在机器学习和数据科学的广阔领域,复杂的算法和模型通常会吸引众人瞩目的焦点。但是,有时候,成功的预测模型的症结不仅仅是选择正确的算法,而且更多地涉及以算法可以最好地学习的方式呈现数据。
这本简短的文章是从我的拖延出生的,它根据数据可视化和转换的力量探索了线性回归模型。我的目标是展示数据表示的简单更改如何改善模型性能。
设置舞台:基本线性回归
为了说明这一点,请考虑一个捕获电视广告与销售之间关系的数据集。我们通过加载数据和可视化关系开始探索。
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
# jupyter labextension install plotlywidget
pd.options.plotting.backend = "plotly"
ADS_DATA_RI = "https://raw.githubusercontent.com/justmarkham/scikit-learn-videos/master/data/Advertising.csv"
dataf = pd.read_csv(ADS_DATA_RI, index_col=0)
# split my data to test the performance of the model
X, y = dataf[["TV"]], dataf["Sales"]
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=.8, random_state=7)
(dataf
.assign(split=lambda d: np.where(d.index.isin(X_train.index), "train", "test"))
.plot(kind="scatter",
x="TV",
y="Sales",
color="split",
trendline="ols",
trendline_scope="overall",
trendline_color_override="darkblue",
opacity=.7,
title="Sales ~ TV Ads")
)
散点图显示了电视广告和销售之间的完全不是线性关系,而我们的线性回归模型并未准确捕获较低价值电视广告支出的销售趋势。
让我们使用scikit-learn进行逆向线性模型方程:
from numpy.typing import NDArray
from sklearn.linear_model import LinearRegression
from sklearn import metrics
lm = LinearRegression(fit_intercept=True)
lm.fit(X_train, y_train)
def get_equation(features:NDArray[str], coef:NDArray[float], intercept:float, y:str="Sales", ) -> str:
equation = " + " .join([*[f"{coef:.5f} * {feature}"
for feature, coef in zip(features, coef)],
f"{intercept:.5f}"])
return f"{y} ~ {equation}"
y_func = get_equation(features=lm.feature_names_in_, coef=lm.coef_, intercept=lm.intercept_)
print(y_func)
# 'Sales ~ 0.04727 * TV + 7.17408'
和R平方分数,该分数了解了我们的模型如何解释响应数据围绕其均值的变异性的方式是:
y_pred = lm.predict(X_test)
R2 = f"{metrics.r2_score(y_true=y_test, y_pred=y_pred):.7f}"
print(R2)
# '0.6779489'
然而,在绘制残差(这是实际值和预测值之间的差异)时,我们观察到一个模式:
...
(pd
.DataFrame(y_test - y_pred)
.rename(columns={"Sales": "Resuduals"})
.assign(TV = X_test,
Position = X_test.index)
.plot(kind="scatter",
y="Resuduals",
x="Position",
title=f"True Sales - Predicted Sales: {R2=} ",
**fig_size
)
.add_hline(y=0)
.update_traces(mode="markers", hovertemplate=None)
.update_layout(hovermode="y unified")
)
残差中的这种模式表明我们的线性模型并不完美。如果我们的模型准确捕获了基础数据的结构,则残差不应表现出任何模式。
我爱贝克汉姆
可视化表明,电视广告与销售之间的关系并非严格线性,但最初似乎是逆指数的。这表明,在广告上花费的第一个 $ 1- $ 50可能会产生较慢的销售回报,然后再拿到势头。
捕获这种潜在关系的一种简单方法是使用对数转换输入(电视广告)和输出(销售)。
# Data Transformation
...
(dataf
.assign(split=lambda d: np.where(d.index.isin(X_train.index), "train", "test"))
.plot(kind="scatter",
x="TV",
y="Sales",
color="split",
trendline="ols",
trendline_options=dict(log_x=True, log_y=True), # power of transformation
trendline_scope="overall",
trendline_color_override="darkblue",
opacity=.7,
title="log(Sales) ~ log(TV) Ads + c",
**fig_size)
)
我们的转换散点图表明,对数转换的电视广告和销售之间有更线性的关系。这清楚地表明,我们关于对数关系的最初假设可能是正确的。
转换线性回归:更合适?
让我们使用对数转换的数据并拟合线性回归模型:
from sklearn.compose import TransformedTargetRegressor
from sklearn.preprocessing import FunctionTransformer
from sklearn.pipeline import make_pipeline
def inverse_log10(X:float)->float:
return 10 ** X
transformer = FunctionTransformer(func=np.log10, inverse_func=inverse_log10)
linear_model = TransformedTargetRegressor(regressor=LinearRegression(), func=np.log10, inverse_func=inverse_log10)
lmx = make_pipeline(transformer, linear_model)
lmx.fit(X_train, y_train)
此新模型的R平方分数是:
y_pred = lmx.predict(X_test)
R2 = f"{metrics.r2_score(y_true=y_test, y_pred=y_pred):.7f}"
print(R2)
# 0.6962380
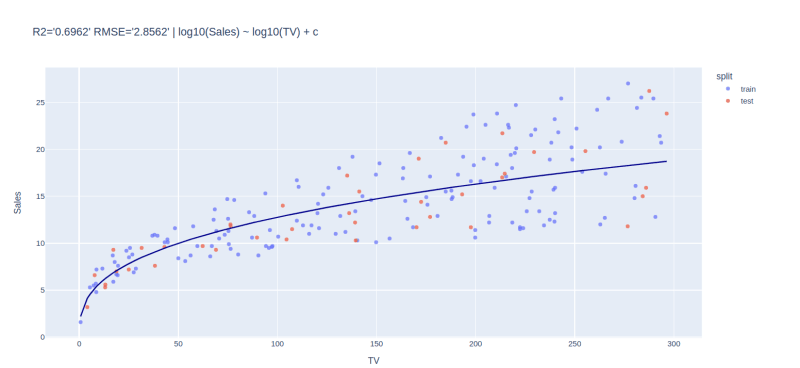
分数高于我们的初始模型(0.67)。它表明我们的转换模型正在解释销售数据中的更多可变性。
与实际数据一起可视化我们的转换模型,我们得到:
(dataf
.assign(split=lambda d: np.where(d.index.isin(X_train.index), "train", "test"))
.plot(kind="scatter",
x="TV",
y="Sales",
color="split",
opacity=.7,
title="log10(Sales) ~ log10(TV) + c",
**fig_size)
).add_traces(
(dataf
.assign(pred = lmx.predict(dataf[["TV"]]))
.sort_values(by=["TV"])
.plot(kind="line",
x="TV",
y="pred",
**fig_size
).update_traces(line_color="darkblue")
).data)
下一步:贝叶斯线性回归模型
我们已经注意到,随着电视广告的大小增加,这些值与我们的拟合线路更加偏离。使用贝叶斯线性回归将是一种更好的方法
要点:ð
这里的主要要点是,预测模型的成功并不总是在于选择更复杂的算法。在达到更复杂的模型之前,请花点时间退后一步,考虑数据转换是否可以简化事物。请记住,有时您需要数据转换。
在此之前,请继续简化数据科学。