介绍:
在此博客中,我们将踏上令人兴奋的迷宫,揭开复杂挑战并找到通往我们目的地的道路的激动人心的旅程。我们冒险的核心是Dijkstra的算法,这是一种强大的工具,它彻底改变了我们解决最短路径问题的方式。
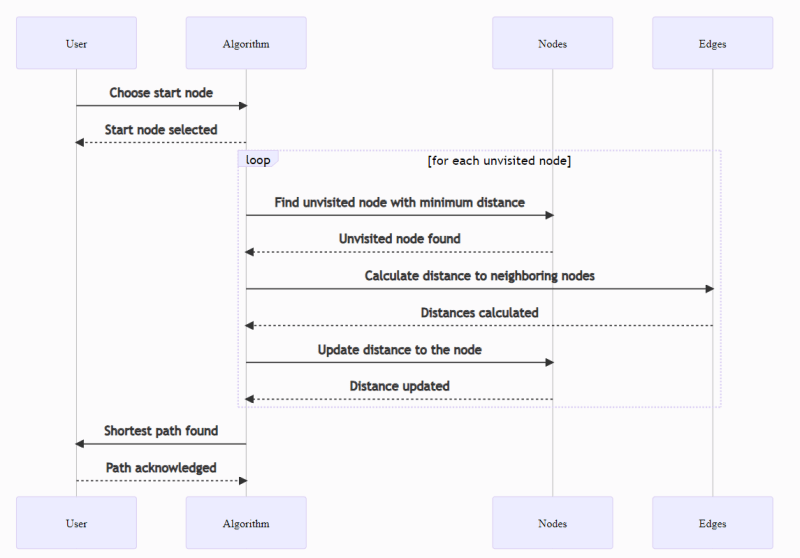
Dijkstra的算法:
想象一下,您有一个有很多街道的大城市,您想找到最短的路径,可以从家里到达自己喜欢的冰淇淋店。 Dijkstra的算法就像一张神奇的地图,可帮助您找到到达目的地的最快方法。首先,您从家开始,然后在地图上标记。然后,您从家里看附近的所有街道,看看走到每个地方需要多长时间到达不同的地方。您写下地图上每条街道的时间。接下来,您搬到街道,步行时间最少,然后将其标记为当前位置。然后,您重复该过程。查看与您当前位置相连的所有街道,并写下每条街道的时间。继续这样做,直到到达冰淇淋店。每次您搬到新位置时,都会增加到达那里所花费的时间。最后,您将拥有从家到冰淇淋店的最短路径!
问题定义:
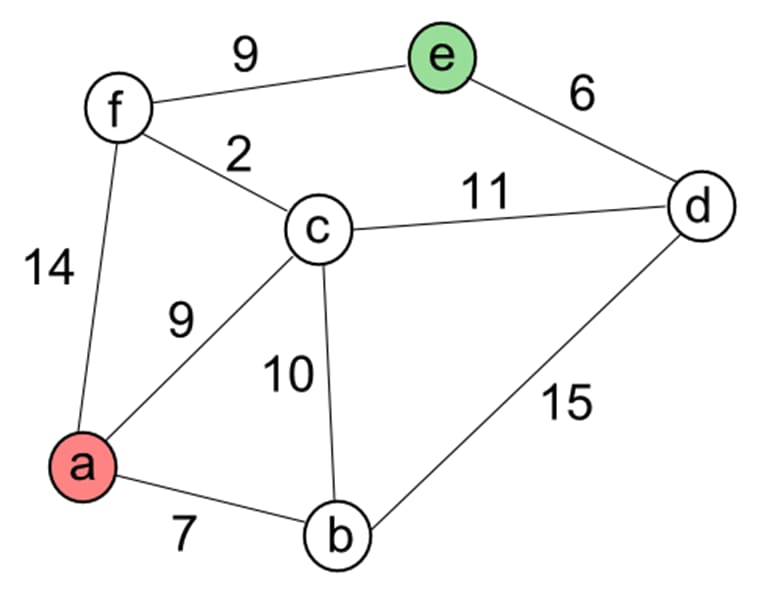
考虑以下图中找到点A和点E之间最短距离的任务
方法1:Excel求解器
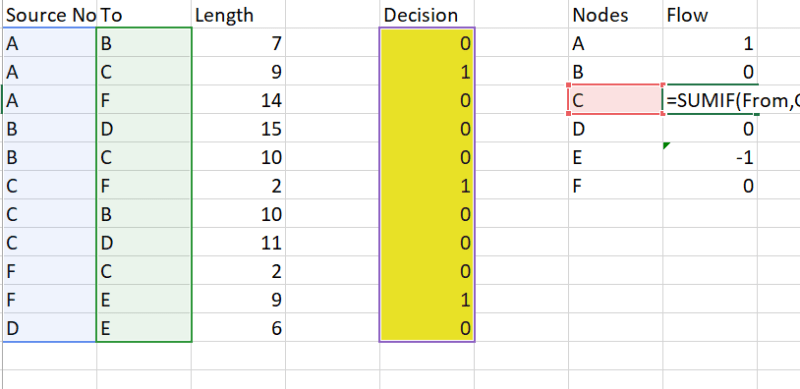
设置:
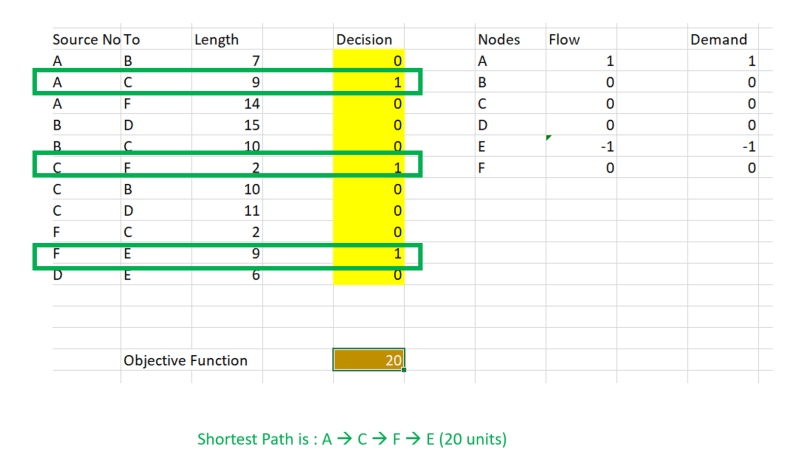
- 决策变量是需要设置活动的节点。它是二进制变量(在黄色细胞中突出显示)
- 目标函数是最大程度地减少源点A和终点B之间的总距离。
- 设置范围。
| 范围名称 | 单元格参考 |
|---|---|
| 来自 | A4:A14 |
| to | b4:b14 |
| 决策 | e4:e14 |
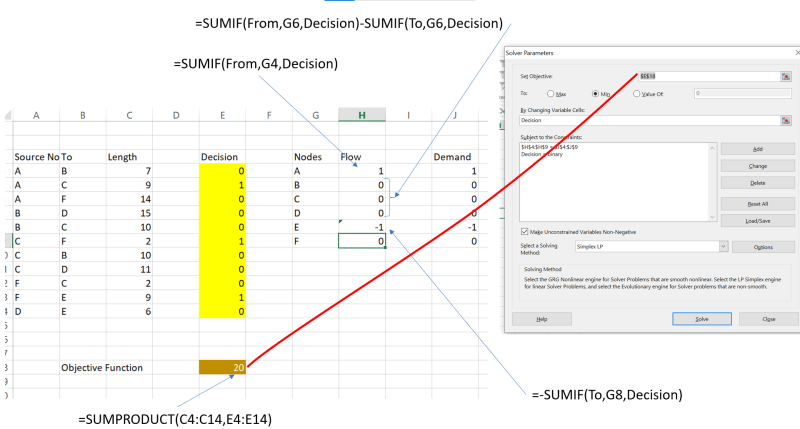
- 约束。每个节点的净流(流出 - 流量)应等于供需。节点A(源节点)应只有一个传出弧(净流= 1)。节点E(目的地)应只有一个ingo弧(净流= -1)。如果节点处于最短路径(net Flow = 0)或无流量(净流= 0)。
Excel求解器设置看起来像这样。
解决方案将如下
方法2:Python
!pip install Dijkstar
from dijkstar import Graph, find_path
graph = Graph ()
graph.add_edge(1, 2, 7)
graph.add_edge(1, 3, 9)
graph.add_edge(1, 6, 14)
graph.add_edge(2, 4, 15)
graph.add_edge(2, 3, 10)
graph.add_edge(3, 6, 2)
graph.add_edge(3, 2, 10)
graph.add_edge(3, 4, 11)
graph.add_edge(6, 3, 2)
graph.add_edge(6, 5, 9)
graph.add_edge(4, 5, 6)
shortest_path = find_path(graph, 1, 5)
#print(graph)
print(shortest_path)
输出
Shortest Path Output: PathInfo(nodes=[1, 3, 6, 5], edges=[9, 2, 9], costs=[9, 2, 9], total_cost=20)
结论:
拥抱Dijkstra算法的魔力,无论您是电子表格爱好者还是编码狂热者,您现在都拥有知识和工具来掌握找到最短的道路并导致成功的方式