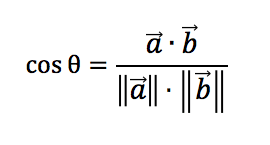在本文中,您将了解什么是余弦相似性以及如何使用Python进行计算。
什么是余弦相似性?
余弦相似性是一种用于衡量两个实体的相似性的度量,无论其大小如何。它测量了在多维空间中投影的两个向量之间的角度的余弦。
在这种情况下,我正在谈论的两个向量是数字数组(例如python中的列表),它们之间的角度是对它们的相似程度的衡量。向量越近,角度越小,导致余弦接近1,反之亦然。该度量是方向的测量(不是幅度)。
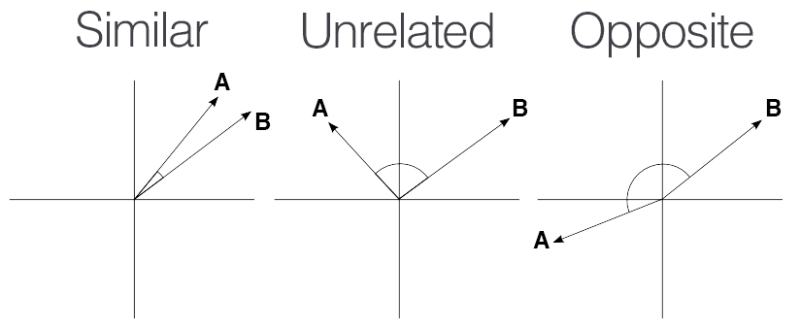
现在,如果箭头处于90度角,则意味着数据集是无关的,余弦相似性为0。因此,简而言之,余弦相似性是一种衡量相关两组数据的方式。相似性范围从-1到1,其中:
- 1表示向量是相同的
- 0表示向量是无关的(不相似)
- -1表示向量是截然相反的(完全不同的)
在上图中,您可以在视觉上看到余弦相似性及其对两个不同矢量的分类。
如果您想了解有关向量的更多信息,我有一篇文章对此进行解释:What is a vector embedding?
余弦的相似性公式
计算余弦相似性的数学公式为:
其中:
a和b是我们的向量
a和b的点产品(a。b)被计算为DOT产品
||a||和||b||是向量的幅度(长度)
用Python计算它
python函数cosine_similarity(vector1: list[float], vector2: list[float]) -> float:采用两个向量作为输入并计算其余弦相似性。
让我们看看完整的代码
from math import sqrt, pow
def cosine_similarity(vector1: list[float], vector2: list[float]) -> float:
"""Returns the cosine of the angle between two vectors."""
# the cosine similarity between two vectors is the dot product of the two vectors divided by the magnitude of each vector
dot_product = 0
magnitude_vector1 = 0
magnitude_vector2 = 0
vector1_length = len(vector1)
vector2_length = len(vector2)
if vector1_length > vector2_length:
# fill vector2 with 0s until it is the same length as vector1 (required for dot product)
vector2 = vector2 + [0] * (vector1_length - vector2_length)
elif vector2_length > vector1_length:
# fill vector1 with 0s until it is the same length as vector2 (required for dot product)
vector1 = vector1 + [0] * (vector2_length - vector1_length)
# dot product calculation
for i in range(len(vector1)):
dot_product += vector1[i] * vector2[i]
# vector1 magnitude calculation
for i in range(len(vector1)):
magnitude_vector1 += pow(vector1[i], 2)
# vector2 magnitude calculation
for i in range(len(vector2)):
magnitude_vector2 += pow(vector2[i], 2)
# final magnitude calculation
magnitude = sqrt(magnitude_vector1) * sqrt(magnitude_vector2)
# return cosine similarity
return dot_product / magnitude
代码开始初始化点乘积的变量和向量的大小。然后,它检查两个输入向量的长度,并用零填充一个较短的长度,以使它们具有相同的长度。此步骤对于计算点产品是必需的。
然后,使用循环计算两个向量的点产物和每个矢量的大小。最后,通过将点产物除以大小的产物来计算余弦相似性。
用法
您可以在代码中使用此功能,如下所示:
Copy code
vector1 = [1, 2, 3]
vector2 = [2, 3, 4]
similarity = cosine_similarity(vector1, vector2)
print("The cosine similarity between vector1 and vector2 is: ", similarity)
结论
如果您想查看有关余弦相似性和代码的更完整的解释,我在YouTube上发布了一个视频,请逐步教授它。