红黑树(RBT)是一种自我平衡的二进制搜索树(BST),可保证用于搜索,插入和删除操作的对数时间复杂性。这种一致性的保证是很大的 - 因为在插入和删除过程中,常规的二进制搜索树可能会变得不平衡,从而导致O(n)的最差时间复杂性,用于搜索,插入和删除操作。
这种低效率不适用于需要快速操作的大型数据集或应用程序。红色树木通过保持平衡来解决标准BST的问题。这有助于维持所有主要任务的快速而稳定的性能。
本文的音调假设您已经熟悉了二进制搜索树。如果不是,我建议您从二进制搜索树文章开始,然后按照下面的链接开始,然后返回并在此处继续:
Deep Dive into Data structures using Javascript - Binary Search Tree
红黑树的解剖
作为BST的变体(二进制搜索树),红黑树继承了BST的基本属性,例如每个节点最多有两个孩子,而左孩子的价值较低,正确的孩子具有更大的价值值比他们的父节点。
将红色树木与普通BST区分开的原因是它们的其他属性和规则,可确保每次操作后树保持平衡。平衡树意味着保证操作的对数时间复杂性。
红黑树中的每个节点都由5个属性组成:
- 值:< / strong>保存节点的值 /数据。
- 左:在左子节点上持有参考(指针)。
- 右:将参考(指针)符合正确的子节点。
- parent:将参考(指针)保存到父节点。
- 颜色:保持节点的颜色值(红色或黑色)。
我们谈论的其他属性是颜色和父属性:
颜色
红色树中的每个节点都是红色或黑色。颜色属性用于帮助维持树中的平衡。通过调整涉及节点颜色的一组规则(红色属性),每次操作后,树保持平衡。
父母
红色树中的每个节点都有一个指向其父节点的指针。此父属性使穿越树并执行旋转变得更加容易,这对于维持红色的特性和确保平衡至关重要。
红黑树规则
为了保持树的始终平衡,方法需要遵循一组称为红黑树属性的规则:
- 每个节点均为红色或黑色:红色树中的每个节点均为彩色或黑色。
- 根节点始终是黑色的:这是维持红黑树高度平衡属性的必要条件。如果根节点是红色的,那么在执行插入和删除时,树可能会变得不平衡。
- 所有叶子(空节点)都被视为黑色:通过将所有空节点视为黑色,我们确保从根节点到叶子节点的每个路径都包含相同数量的黑色节点。
- 不允许两个连续的红节点,即红节点的孩子必须是黑色的:这被称为“红色节点属性”。如果要连续出现两个红色节点,则在执行插入和删除时,树可能会变得不平衡。
- 从节点到其后代无效节点的每个路径都包含相同数量的黑色节点:这被称为“黑色节点属性”。通过确保从节点到其后代null节点的每个路径都包含相同数量的黑色节点,树的高度始终保持在节点数量中。
!»»查看下面的视觉效果,以查看这些规则如何适用于红黑树:
红黑树如何保持平衡?
通过执行我们上面讨论的属性,保持红色树的平衡。让我们仔细研究这些特性如何在高水平上促进树的平衡:
颜色特性(红色或黑色)通过防止连续的红节点来帮助控制树的高度:这确保了从根到最远的叶子的路径不长,因为它可以防止形成红色节点的长链。
黑色高度属性可确保从节点到其后代无效节点的每条路径都具有相同数量的黑色节点:这确保最长的路径不超过最短长度的两倍路径,保持树的平衡。
当插入新节点或删除现有节点时,红色树可能会暂时侵犯这些属性。为了恢复树的平衡,执行了一系列的旋转和颜色变化,称为“重新平衡操作”。这些操作保留了红黑树的特性,以使树保持平衡。
何时使用红黑树
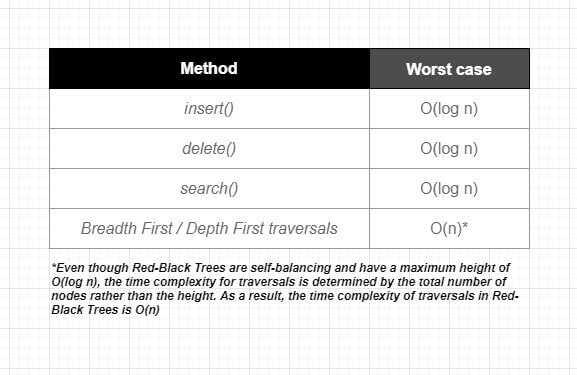
lï»»et he et tok the Red-Black Tree中的普通操作的Big O。
sﻀince始终保持平衡并保持O(log n)的高度,所有关键操作(例如插入,删除和搜索)的时间复杂性始终是O(log n),而没有边缘情况。与二进制搜索树相比,这是一个重要的优势,因为它们可能变得不平衡,这会导致这些操作的O(n)的最差时间复杂性。
当涉及到广度优先和深度优先的遍历时,就像其他类型的树一样,它们具有O(n)(线性时间)的时间复杂性。尽管红黑树是自动平衡,最大高度(log n),但遍历的时间复杂性取决于节点的总数而不是高度。因此,红黑树中遍历的时间复杂性也为o(n)。
插入 /删除 /搜索操作的效率在某些情况下使红色树木具有强大的工具,特别是在处理大型数据集并需要有效操作时。一些红黑树有意义的用例:
有效的搜索操作:
在数据检索频繁且关键的情况下,红黑树可带来重大好处。将此数据结构集成到数据库索引或面向对象的数据库中可以极大地提高搜索查询速度。
例如,考虑一家大型在线书店,其中包含数百万本书的库存。每当客户在网站上搜索一本书时,系统都需要快速从数据库中检索相关的书籍信息并显示结果。
通过使用红黑树作为索引结构,书店可以根据钥匙(例如书的标题或作者)以分类方式存储有关每本书的信息。结果,书店可以有效地检索书籍信息,从而为客户提供更快的搜索结果。这不仅可以改善用户体验,还可以减少数据库服务器上的负载,因为它可以使用红黑树索引结构更有效地处理搜索查询。
动态数据处理:
当使用插入和删除的动态数据集时,红黑树表明了它们的力量。考虑一个在线交易平台,用户可以在其中买卖股票。该平台可实时处理大量的买卖订单。红黑树可用于有效管理和处理这些订单。
当用户发布买卖订单时,交易平台可以利用红黑树来根据价格或其他相关标准对订单进行排序。例如,当用户想要执行购买订单时,该平台可以通过穿越红黑树来有效地以最低的价格找到最佳的卖出订单。同样,当用户想执行卖出订单时,该平台可以从红黑树中的买入订单中识别出最高的出价。
使用红黑树使交易平台能够将买家与卖家快速匹配,从而确保有效而准确的订单执行。红黑树的平衡性质允许快速搜索操作,并更容易识别最有利的买卖订单。
有序数据操作:
在维持有序元素序列至关重要的用例中,红黑树是理想的选择。例如,在时间序列的数据库中,在该数据库中通过时间戳组织数据,红色树木可以确保按时间顺序排列,同时保持快速插入和删除时间。
考虑一个社交媒体平台,该平台将用户的帖子存储在时间序列数据库中。每个帖子都与时间戳相关联,该时间戳指示何时创建。在这种情况下,可以利用红色树木有效处理帖子的有序顺序。
通过使用红黑树作为基础数据结构,社交媒体平台可以确保根据时间戳按时间扫描以时间顺序存储帖子。这允许在正确的顺序中轻松检索和显示帖子。
用户创建新帖子时,该平台可以利用红黑树快速将帖子插入适当的位置,并保持时间顺序。同样,如果用户删除了帖子,则红黑树可在保留其余帖子的同时有效地删除帖子。
在红黑树的帮助下,社交媒体平台可以为用户提供无缝的浏览体验。用户可以轻松地按照正确的时间顺序浏览帖子,无论他们是在自己的时间轴上滚动还是探索其他用户的帖子。
语言库:
红色树木通常在众多编程语言的标准库中使用。例如,C ++在其STL(标准模板库)中使用红色树木进行地图和设置数据结构,为这些抽象提供了有效的实现。
数据库系统:
数据库通常使用红黑树进行索引。这些数据结构提供了快速访问,从而允许数据库迅速检索记录。当处理涉及多个属性并需要最佳性能的复杂查询时,这一点尤其重要。
eï»»ven尽管红色树木非常通用,但它们不是“千篇一律的”解决方案。根据系统的特定要求,其他数据结构可能更合适。关键是要了解问题的性质和您需要经常执行的操作,然后相应地选择最合适的数据结构。
rﻀed-black树vs avl树
iï»f,您发现自己处于想要使用红色树木的情况下,很可能您会寻找一种自动平衡的二进制搜索树的变化。 tï»»这是vish»。
eï»»虽然两者都是自动平衡,但在某些情况下,一个比另一个是优先的。
选择一棵红黑树时:
- 插入和删除频繁:在插入和删除后平衡红色树的过程通常比旋转较少的旋转速度要快,而AVL树的过程比AVL树的过程更快,这使其成为更高的写入工作量的更好选择。
- 记忆是一个关注的:红色树木通常需要比AVL树更少的空间,因为它们只需要在每个节点上存储一个信息(颜色)。
- 适度的搜索时间是可以接受的:虽然RBT确实确保了搜索时间O(log n)的上限,但由于其更严格的平衡,AVL树通常提供更快的查找。如果您的应用程序可以忍受更长的搜索时间以更快的写入或更少的记忆使用情况,则RBT可能是一个不错的选择。
选择一棵AVL树时:
- 查找频繁:AVL树比红黑树更严格平衡,这意味着它们通常提供更快的查找时间。如果您的应用程序涉及的读取操作多于写操作,则AVL树可能是一个更好的选择。
- 始终快速搜索时间至关重要:如果您的用例需要持续快速搜索时间,并且更新的频率(插入和删除)相对较低,则AVL树将是一个更合适的选择。
- 插入和删除很少:虽然AVL树的更新可能比红黑树慢,但如果更新在您的应用程序中相对较少,这可能不是一个重要因素。
aï»t结束时,红色树木和AVL树之间的选择通常取决于您应用程序的特定需求,包括不同操作的相对频率,快速搜索时间和内存使用限制的重要性。
javaScript中的ed-black树实现
我们将使用ES6类来构建我们的红黑树。这是我们要实现的方法列表:
-
insert(value)-此方法用于将新值插入红黑树中。该方法首先创建一个新节点并将其放置在正确的位置,就像在标准的二进制搜索树中一样。插入节点后,调用_insertFixup方法来还原红色树属性。 -
_insertFixup(node)-这是一种助手方法,用于确保插入操作后保持红黑树特性。该方法调整节点的颜色并根据需要进行旋转,直到树平衡并遵循红色树规则。 -
delete(value)-此方法从树上删除带有给定值的节点。它首先使用搜索方法找到节点,然后在维护红色树属性的同时将其删除。删除节点后,_deleteFixup方法被调用以还原红色树属性。 -
_deleteFixup(node)-这是一种助手方法,用于确保删除操作后保持红色树特性。与_insertFixup方法类似,它调整节点的颜色并根据需要执行旋转,直到树平衡并遵循红色树规则。 -
search(value)-此方法在树上找到与给定值匹配的节点。它在删除操作期间用于查找需要删除的节点。 -
_replaceParent(curNode, newNode)-此助手方法用于用新节点替换给定节点的父。它在旋转和节点删除过程中使用。 -
_leftRotation(node) and _rightRotation(node)-这些是用于执行树上左右旋转的辅助方法。它们在插入过程中使用并删除操作以维护红黑树的特性。 -
_flipColor(node)-一种辅助方法,可以改变节点及其子女的颜色。它在插入和删除操作期间用于维护红黑树特性。 -
_isRed(node)-一种辅助方法,检查节点是否为红色。此方法用于各种操作来确定特定节点的颜色。 -
findMin(node)-此方法找到树中最小值的节点。它在删除操作期间用于查找被删除的节点的继任者。 -
levelOrderTraversal()-将rï»»显示为级别的多维数组,uï»»唱歌级别的顺序遍历。最终输出数组将代表每个子阵列代表树的水平。
我想第一次注意到红黑树将是一个坚实的挑战,因为它们位于数据结构频谱的高级且复杂的端。充分掌握所有概念将需要投入时间进行实验和探索。红黑树的力量置于“维持平衡”因子(这是关键概念)之内 - 但它以实施复杂性为代价。
研究插入和删除方法时,您将查看许多条件和步骤 - 这些条件和步骤与红黑树特定操作(例如旋转和颜色翻转)结合使用。了解这些操作至关重要,因为它们构成了红黑树在插入和删除过程中如何保持平衡的核心机制。
旋转(左右)和颜色翻转是关键操作,每当由于插入或删除而违反树的属性时,有助于重新平衡该树。他们一起工作以重新排列节点并更改其颜色以恢复红黑树的特性。首先了解这些操作的工作方式将使更容易理解更复杂的插入和删除方法。
要可视化并更好地了解红黑树的机制,我强烈建议您在下面的链接下使用这个惊人的红色树木可视化器来玩耍:
我希望这篇文章能帮助您为什么是红色树木以及它们的工作方式奠定良好的基础!我想鼓励您在您喜欢的代码编辑器中尝试以下实现。感谢您的阅读!
javaScript中红色树的implementation
const NodeColor = {
RED: 'RED',
BLACK: 'BLACK',
}
class RBTNode {
constructor(value, parent = null) {
this.value = value
this.left = null
this.right = null
this.parent = parent
this.color = NodeColor.RED
}
}
class RedBlackTree {
constructor() {
this.root = null
}
insert(value) {
// Define an inner helper function for the recursive insertion
const insertHelper = (node) => {
// The current node we're considering
const currNode = node
// If the value to insert is less than the value of the current node
if (value < currNode.value) {
// If a left child node exists, recursively call 'insertHelper' on it
if (currNode.left) {
insertHelper(currNode.left)
} else {
// If no left child node exists, create a new node with the value
// Make the new node a left child of the current node
// The color of the new node is red by default (from the RBTNode constructor)
currNode.left = new RBTNode(value)
// Set the parent of the new node to be the current node
currNode.left.parent = currNode
// Call the helper method '_insertFixup' to maintain Red-Black Tree properties after insertion
this._insertFixup(currNode.left)
}
} else if (value > currNode.value) {
// If the value to insert is greater than the value of the current node
// If a right child node exists, recursively call 'insertHelper' on it
if (currNode.right) {
insertHelper(currNode.right)
} else {
// If no right child node exists, create a new node with the value
// Make the new node a right child of the current node
// The color of the new node is red by default (from the RBTNode constructor)
currNode.right = new RBTNode(value)
// Set the parent of the new node to be the current node
currNode.right.parent = currNode
// Call the helper method '_insertFixup' to maintain Red-Black Tree properties after insertion
this._insertFixup(currNode.right)
}
}
// If the value is equal to the current node's value, we do nothing because
// duplicates are not typically allowed in binary search trees
}
// If the tree is empty (no root node)
if (!this.root) {
// Create a new root node with the value
// The color of the new root node is red by default (from the RBTNode constructor)
this.root = new RBTNode(value)
// Call the helper method '_insertFixup' to maintain Red-Black Tree properties after insertion
// In this case, it will simply recolor the root to black
this._insertFixup(this.root)
} else {
// If the tree is not empty, call the 'insertHelper' function on the root node
insertHelper(this.root)
}
}
// Helper method to maintain tree balance after an insertion
_insertFixup(node) {
// Start with the node that was just inserted
let currNode = node
// While the parent of the current node is red and the grandparent exists
// This loop maintains the property that no two red nodes will be adjacent
while (this._isRed(currNode.parent) && currNode.parent.parent) {
// Define some helper variables to make the code more readable
const { parent } = currNode
const grandparent = parent.parent
// If the parent of the current node is a left child
if (parent === grandparent.left) {
// If the uncle (the right child of the grandparent) is red
if (this._isRed(grandparent.right)) {
// Flip the colors of the parent, grandparent, and uncle
// This maintains the property that every path from a node to its descendant leaves contains the same number of black nodes
this._flipColor(grandparent)
} else {
// If the uncle is black or null
// If the current node is a right child, do a left rotation to make it a left child
// This is done to prevent two red nodes from being adjacent
if (currNode === parent.right) {
this._leftRotation(parent)
// After the rotation, the current node and its parent are swapped
currNode = parent
}
// Perform a right rotation on the grandparent
// This makes the former parent (a red node) the parent of its former parent (a black node)
// This maintains the property that every path from a node to its descendant leaves contains the same number of black nodes
this._rightRotation(grandparent)
}
} else {
// The mirror case when the parent of the current node is a right child
// The code is the same except that 'left' and 'right' are exchanged
if (this._isRed(grandparent.left)) {
this._flipColor(grandparent)
currNode = grandparent
} else {
if (currNode === parent.left) {
this._rightRotation(parent)
currNode = parent
}
this._leftRotation(grandparent)
}
}
// Move up the tree
currNode = grandparent
}
// Ensure the root is always black to maintain the black-root property
this.root.color = NodeColor.BLACK
}
delete(value, node = this.root) {
// Search the tree to find the target node
const targetNode = this.search(value, node)
// If the target node is not found, return false
if (!targetNode) {
return false
}
// If the target node has no children (leaf node)
if (!targetNode.left && !targetNode.right) {
// If the target node is red, simply remove it by replacing it with null in its parent
// Red nodes can be removed freely because removing them doesn't affect the black height property
if (this._isRed(targetNode)) {
this._replaceParent(targetNode, null)
} else {
// If the target node is black, removal would affect black height property
// Hence, we need to call '_deleteFixup' to fix the potential violations
this._deleteFixup(targetNode)
// After that, we can remove the black node
this._replaceParent(targetNode, null)
}
} else if (!targetNode.left || !targetNode.right) {
// If the target node has only one child (unilateral subtree)
if (targetNode.left) {
// If the child is on the left, set the child's color to black
// The color is set to black to maintain the black height property
targetNode.left.color = NodeColor.BLACK
// Update the parent pointer of the child
targetNode.left.parent = targetNode.parent
// Replace the target node with its child
this._replaceParent(targetNode, targetNode.left)
} else {
// Similar operations for the right child
targetNode.right.color = NodeColor.BLACK
targetNode.right.parent = targetNode.parent
this._replaceParent(targetNode, targetNode.right)
}
} else {
// If the target node has two children
// Find the node with the smallest value that is larger than the value of the target node (aux)
// This node is used to replace the target node
const aux = this.findMin(targetNode.right)
// Replace the value of the target node with the value of the aux node
targetNode.value = aux.value
// Delete the aux node recursively
// The aux node will have at most one child, so this deletion is easier
this.delete(aux.value, targetNode.right)
}
// Return the root of the tree after deletion
return this.root
}
// Helper method to maintain tree balance after a deletion
_deleteFixup(node) {
// 'currNode' is the node to be fixed
let currNode = node
// Loop until 'currNode' is the root or 'currNode' is red
while (currNode !== this.root && !this._isRed(currNode)) {
// Get the parent of 'currNode'
const { parent } = currNode
// Define 'sibling', which will be the sibling of 'currNode'
let sibling
// If 'currNode' is a left child
if (currNode === parent.left) {
// 'sibling' is the right child of 'parent'
sibling = parent.right
// If the 'sibling' is red
if (this._isRed(sibling)) {
// Perform left rotation on 'parent'
this._leftRotation(parent)
}
// If both children of 'sibling' are black
else if (!this._isRed(sibling.left) && !this._isRed(sibling.right)) {
// If 'parent' is red
if (this._isRed(parent)) {
// Swap colors of 'parent' and 'sibling'
parent.color = NodeColor.BLACK
sibling.color = NodeColor.RED
// Fixup is done because 'currNode' now has an additional black link
break
}
// If 'parent' is black, make 'sibling' red
sibling.color = NodeColor.RED
// Move up the tree
currNode = parent
}
// If 'sibling's left child is red and right child is black
else if (this._isRed(sibling.left) && !this._isRed(sibling.right)) {
// Perform right rotation on 'sibling'
this._rightRotation(sibling)
}
// If 'sibling's right child is red
else {
// Perform left rotation on 'parent'
this._leftRotation(parent)
// Change color of 'parent' and 'sibling's right child to black
parent.color = NodeColor.BLACK
sibling.right.color = NodeColor.BLACK
// Fixup is done because 'currNode' now has an additional black link
break
}
}
// If 'currNode' is a right child, similar operations are performed with 'left' and 'right' interchanged
else {
sibling = parent.left
if (this._isRed(sibling)) {
this._rightRotation(parent)
} else if (!this._isRed(sibling.left) && !this._isRed(sibling.right)) {
if (this._isRed(parent)) {
parent.color = NodeColor.BLACK
sibling.color = NodeColor.RED
break
}
sibling.color = NodeColor.RED
currNode = parent
} else if (this._isRed(sibling.right) && !this._isRed(sibling.left)) {
this._leftRotation(sibling)
} else {
this._rightRotation(parent)
parent.color = NodeColor.BLACK
sibling.left.color = NodeColor.BLACK
break
}
}
}
}
search(value, node = this.root) {
// Check if the current node is null (reached a leaf node or an empty tree)
if (!node) {
// Value not found, return false
return false
}
// Check if the current node's value matches the search value
if (value === node.value) {
// Value found, return the node
return node
}
// If the search value is less than the current node's value, go to the left subtree
if (value < node.value) {
// Recursively call the search function on the left child node
return this.search(value, node.left)
}
// If the search value is greater than the current node's value, go to the right subtree
// This assumes the tree follows the convention of left child nodes having lesser values and right child nodes having greater values
return this.search(value, node.right)
}
/*
This method is used to replace the parent of a given node with a new node. It is primarily used during node deletion and rotation operations. When a node is deleted or when rotations are performed, it may be necessary to update the parent reference of a child node to point to a new node.
*/
_replaceParent(currNode, newNode) {
// Get the parent node of the current node
const { parent } = currNode
// Check if the current node is the root node (no parent)
if (!parent) {
// If so, set the new node as the new root of the tree
this.root = newNode
}
// If the current node is the left child of its parent
else if (currNode === parent.left) {
// Set the new node as the left child of the parent
parent.left = newNode
}
// If the current node is the right child of its parent
else {
// Set the new node as the right child of the parent
parent.right = newNode
}
}
/*
A helper method that performs a left rotation on the tree structure.
Left rotation is an operation that repositions the nodes in the tree
to maintain its properties when they have been disturbed, for example, during insertion or deletion.
It is used when the right child of a node is colored red. The operation involves repositioning
the node and its right child, and updating the colors of the nodes accordingly. After a left rotation, the
former parent becomes the left child of its former right child.
This method should be called when it is safe to do a left rotation, that is, when the right child is not null.
*/
_leftRotation(node) {
// 'currNode' is set as the right child of 'node'
const currNode = node.right
// The left child of 'currNode' becomes the right child of 'node'
node.right = currNode.left
// 'node' becomes the left child of 'currNode'
currNode.left = node
// The color of 'currNode' is set as the color of 'node'
currNode.color = node.color
// The color of 'node' is set as red
node.color = NodeColor.RED
// The parent of 'node' is replaced with 'currNode'
this._replaceParent(node, currNode)
// The parent of 'currNode' is set as the parent of 'node'
currNode.parent = node.parent
// 'node' becomes the child of 'currNode'
node.parent = currNode
// If 'node' has a right child, the parent of the right child is set as 'node'
if (node.right) {
node.right.parent = node
}
}
/*
A helper method that performs a right rotation on the tree structure.
Right rotation is an operation that repositions the nodes in the tree
to maintain its properties when they have been disturbed, for example, during insertion or deletion.
It is used when the left child of a node is colored red. The operation involves repositioning
the node and its left child, and updating the colors of the nodes accordingly. After a right rotation, the
former parent becomes the right child of its former left child.
This method should be called when it is safe to do a right rotation, that is, when the left child is not null.
*/
_rightRotation(node) {
// 'currNode' is set as the left child of 'node'
const currNode = node.left
// The right child of 'currNode' becomes the left child of 'node'
node.left = currNode.right
// 'node' becomes the right child of 'currNode'
currNode.right = node
// Update color: The color of 'currNode' is set as the color of 'node'
currNode.color = node.color
// The color of 'node' is set as red
node.color = NodeColor.RED
// Update parent node: The parent of 'node' is replaced with 'currNode'
this._replaceParent(node, currNode)
// The parent of 'currNode' is set as the parent of 'node'
currNode.parent = node.parent
// 'node' becomes the child of 'currNode'
node.parent = currNode
// If 'node' has a left child, the parent of the left child is set as 'node'
if (node.left) {
node.left.parent = node
}
}
/*
Helper method that changes the color of a node and its children.
The concept here is to change the color of the parent node to red, and the color of the two child nodes to black.
This color flip is part of the process that helps to maintain the properties of a Red-Black Tree, which include keeping the tree balanced and ensuring that no two red nodes are adjacent, among others.
Please note that before calling this method, you should check that both children of the node are present and their colors are red. This method assumes this condition is met.
*/
_flipColor(node) {
// The color of the current node is set to RED
node.color = NodeColor.RED
// The color of the left child of the current node is set to BLACK
node.left.color = NodeColor.BLACK
// The color of the right child of the current node is set to BLACK
node.right.color = NodeColor.BLACK
}
// Helper method to check the node color
_isRed(node) {
return node ? node.color === NodeColor.RED : false
}
// Helper method that finds the node with the smallest value in the tree. It's used during the delete operation to find the successor of a node that's being deleted.
findMin(node = this.root) {
let currentNode = node
while (currentNode && currentNode.left) {
currentNode = currentNode.left
}
return currentNode
}
// Displays an array that will represent the tree
// in level-order, with each sub-array representing a level of the tree.
levelOrderTraversal() {
// Create an empty array to store the traversed nodes
const temp = []
// Create an array to keep track of the current level of nodes
const queue = []
// If the tree has a root, add it to the queue
if (this.root) {
queue.push(this.root)
}
// Keep traversing the tree while there are nodes in the queue
while (queue.length) {
// Create an array to store the nodes of the current level
const subTemp = []
// Store the number of nodes in the current level
const len = queue.length
// Iterate through the current level of nodes
for (let i = 0; i < len; i += 1) {
// Dequeue the first node in the queue
const node = queue.shift()
// Push the node's value to the subTemp array
subTemp.push(node.value)
// If the node has a left child, add it to the queue
if (node.left) {
queue.push(node.left)
}
// If the node has a right child, add it to the queue
if (node.right) {
queue.push(node.right)
}
}
// Push the subTemp array to the temp array
temp.push(subTemp)
}
// Return the final temp array
return temp
}
}
export default RedBlackTree