图是由边缘(或拱形)连接的体内(或段落)组成的数据结构。它们被广泛用于徒劳,例如计算,数学,狂热,生物学等。
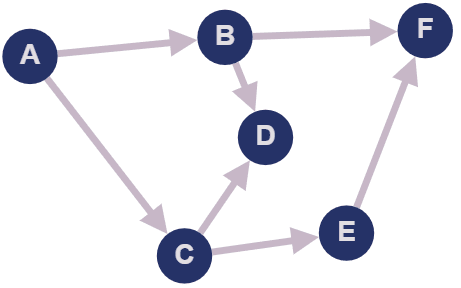
例如,在计算科学中,用于表示对象之间的关系,例如社交网络上的往常,或在地图中建模路线和路径,例如Google地图上的街道。它们允许大量的复杂数据矮人,从而发现模式和信息。让我们看以下图:
回答诸如“ ”诸如Vanice B?b的虚荣心之路?他从vâ©rtice a开始,并将其研究扩展到与他相关的vitices。然后,前进到与b和c相连的剂量,依此类推,以寻求宽度。
。让我们使用JavaScript创建一个宽度研究算法的示例,以回答以下问题: Vanice到Vanice F?
首先,让我们将其定义为对象: 我们说的是它与b和c连接,B与A,D和F等连接。
现在让我们开始创建我们的算法。首先,我们需要他为所有图表的货物做一个循环,并确定访问了哪一个。 现在我们需要让每个新的虚荣心寻求,该功能获得了连接到它的先前的虚荣心,并将路径添加到我们的koud0对象。 现在,该算法已经寻求我们图形的所有味道,我们需要获取它才能获得目的地的徒劳,并且从koud0对象开始,将其构建回起点。>>>>>>>>>>>>
执行我们的方式时,我们会看到搜索结果: 我们可以看到,从徒劳到事实的最短方法是 a-> b-> f
const connections = {
A: [ 'B', 'C' ],
B: [ 'A', 'D', 'F' ],
C: [ 'A', 'D', 'E' ],
D: [ 'B', 'C' ],
F: [ 'B', 'E' ],
E: [ 'C', 'F' ]
}
function findShortestPath(graph, startNode, endNode) {
// fila dos vertices que serão visitados
const queue = [startNode];
// objeto contendo os vértices que já foram visitados
const visited = { [startNode]: true };
// objeto que vai identificar quais os vértices anteriores a um determinado vértice pra montarmos o caminho
const predecessor = {};
// Loop enquanto houverem vértices para ser visitados
while (queue.length) {
// Obtém e remove o primeiro vértice da lista
const currNode = queue.shift();
// RESTO DO NOSSO ALGORITMO
}
return null;
}
function findShortestPath(graph, startNode, endNode) {
const queue = [startNode];
const visited = { [startNode]: true };
const predecessor = {};
while (queue.length) {
const currNode = queue.shift();
// Obtém os vértices que estão conectados ao vértice atual
// aqui são chamados de vizinhos
const neighbors = graph[currNode];
// Itera sobre cada vértice vizinho
for (const neighbor of neighbors) {
// Apenas continua a busca se ele ainda não tiver sido visitado
if (!visited[neighbor]) {
visited[neighbor] = true;
// Adiciona no objeto predecessor o vértice que está ligado a ele
predecessor[neighbor] = currNode;
// Adiciona ele mesmo na fila de vértices para serem pesquisados
queue.push(neighbor);
// RESTO DO NOSSO ALGORITMO
}
}
}
function findShortestPath(graph, startNode, endNode) {
const queue = [startNode];
const visited = { [startNode]: true };
const predecessor = {};
while (queue.length) {
const currNode = queue.shift();
const neighbors = graph[currNode];
for (const neighbor of neighbors) {
if (!visited[neighbor]) {
visited[neighbor] = true;
predecessor[neighbor] = currNode;
queue.push(neighbor);
// Observa se o vizinho que está sendo checado atualmente...
// é o nosso destino
if (neighbor === endNode) {
// Começa a reconstruir o caminho mais curto a partir do vértice...
// de chegada
const shortestPath = [endNode];
// Obtém o vértice atual de onde os vizinhos foram obtidos
let prevNode = currNode;
// Loop enquanto o caminho ainda não tiver sido reconstruído...
// até o ponto de partida
while (prevNode !== startNode) {
// Adiciona no começo da array `shortestPath` o vértice `prevNode`
shortestPath.unshift(prevNode);
// Obtém o predecessor do `prevNode` e faz dele o `prevNode` atual
prevNode = predecessor[prevNode];
}
shortestPath.unshift(startNode);
return shortestPath;
}
}
}
}
return null;
}
const connections = {
A: [ 'B', 'C' ],
B: [ 'A', 'D', 'F' ],
C: [ 'A', 'D', 'E' ],
D: [ 'B', 'C' ],
F: [ 'B', 'E' ],
E: [ 'C', 'F' ]
}
const shortestPath = findShortestPath(connections, 'A', 'F');
console.log(shortestPath); // ['A', 'B', 'F']
宽度搜索算法是解决问题的问题,涉及一个图中两个点之间的最小路径。但是,重要的是要记住,每个应用程序都可以具有其特殊性,并且宽度研究算法不是等级,并且在许多情况下可能不是最小路径的最佳搜索算法。
知道如何实施宽度研究算法可以帮助解决各个领域的复杂问题,例如运输网络,路线优化甚至游戏。