目录
关于气泡排序
气泡排序是一种简单的排序算法,反复逐步浏览要排序的列表。它比较每对相邻项目,并将它们交换为正确的顺序。
还知道其效率低下和O(n^2)的时间复杂性。
气泡排序算法
让我们排序一个数字(整数)[5,1,4,3]。
使该算法更易于解释,让我们可以看到高度代表值的数组。
该算法涉及循环和比较两个值。例如,在4值数组中,我们将最多循环3次,因为我们比较J和J+1。
。在我们的示例中(脚本在下面):
$i = value of outer loop
$j = value of inner loop
$a[$j] = value of an array at the position of $j
$a[$j+1] = value of an array at the position of $j+1
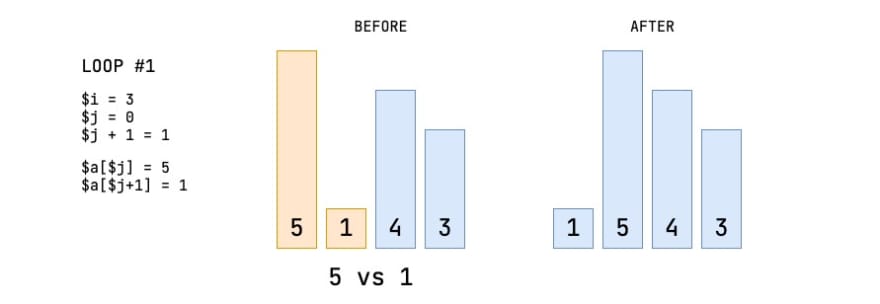
比较#1
我们从数组的开头开始,并比较前两个元素5和1(之前)。由于5大于1,因此我们将它们交换(之后)。
比较#2
我们在循环中递增J的值,并比较接下来的两个元素5和4(之前)。由于5大于4,因此我们将它们交换(之后)。
比较#3
我们在循环中递增J的值,并比较接下来的两个元素5和3(之前)。由于5大于3,因此我们将它们交换(之后)。
注意 :重要的是要注意,最高数字5现在处于正确的排序位置,不需要再次比较。在下一个循环中,我们只需要循环2次,而不是3次(数组减1中的元素总数)。
比较#4
我们的第一个循环完成后,我们将从数组的开头重新开始。我们比较前两个元素1和4(之前)。由于1不大于4,因此我们在循环中继续无需交换它们(之后)。
。比较#5
我们在循环中递增J的值,并比较接下来的两个元素4和3(之前)。由于4大于3,因此我们将它们交换。我们跳过数字5,因为它已经处于排序位置(之后)。
数字5已经排序,所以我们跳过了。
比较#6
在我们的最后一个循环中,我们比较前两个元素1和3(之前)。由于1不大于3,因此我们在循环中继续无需交换它们(之后)。
最终数组看起来像这样(之后):[1、3、4、5]。
功能
循环
要比较数组中的两个值,我们需要一个循环中的循环。
而不是以传统方式循环:
for ($i = 0; $i < count($a) - 1; $i++) { // outer loop
for ($j = $i + 1; $j < count($a); $j++) { // inner loop
// ...
}
}
我们在相反的方向上做到这一点,在外循环中减小,因此我们可以跳过最后排序的数字。
for ($i = count($a) - 1; $i > 0; $i--) { // outer loop
for ($j = 0; $j < $i; $j++) { // inner loop
// ...
}
}
交换
在循环中,我们检查两个值,如果$a[$j] > $a[$j + 1]进行交换。
if ($a[$j] > $a[$j + 1]) {
$temp = $a[$j];
$a[$j] = $a[$j+1];
$a[$j+1] = $temp;
}
气泡排序算法
function bubbleSort(array $a): array
{
for ($i = count($a) - 1; $i > 0; $i--) {
for ($j = 0; $j < $i; $j++) {
if ($a[$j] > $a[$j + 1]) {
$temp = $a[$j];
$a[$j] = $a[$j+1];
$a[$j+1] = $temp;
}
}
}
return $a;
}
// $bs = [5, 2, 8, 9, 1];
// bubbleSort($bs);
// [1, 2, 5, 8, 9]
优化版本
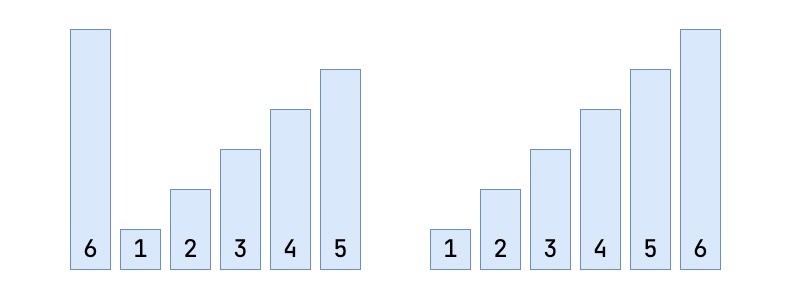
但是,如果我们有几乎对数组(左侧)几乎分类的情况,并且在外循环完成后,我们将所有项目排序。
如果我们使用了上面的脚本,则对于阵列[6、1、2、3、4、5],我们将进行 15比较。但是,很明显,在第一个循环后,所有数字都进行了排序,这意味着我们不必再循环[1、2、3、4、5、6]几次。
我们可以通过跟踪在外循环期间是否进行任何掉期来优化这一点。如果没有互换,我们可以打破循环并返回数组,因为现在已经对其进行排序。
因此,我们再次循环,如果没有交换,我们可以打破循环并返回数组,因为所有数组均已排序。
说明:
- 让我们在外循环中定义一个可变的
$swap。 - 如果条件中有互换,我们将
$swap设置为true。 - 如果外循环中没有交换,我们不需要检查其余的,因此我们打破循环并返回排序的数组。
以下优化仅具有 9的比较对于阵列[6,1,2,3,4,5]。它跳过$ i = 3、2和1的循环。
function bubbleSortOptimized(array $a): array
{
for ($i = count($a) - 1; $i > 0; $i--) {
$swap = false;
for ($j = 0; $j < $i; $j++) {
if ($a[$j] > $a[$j + 1]) {
$temp = $a[$j];
$a[$j] = $a[$j+1];
$a[$j+1] = $temp;
$swap = true;
}
}
if (!$swap) break;
}
return $a;
}
// $bs = [6, 1, 2, 3, 4, 5];
// bubbleSortOptimized($bs);
// [1, 2, 3, 4, 5, 6]
脚本
两个脚本都可以在这里找到:https://gist.github.com/matusstafura/7b049a323624a99a9f0120492888621e
时间复杂性
气泡排序的时间复杂性在最坏的情况和平均情况下为O(n^2),在最佳情况下为O(n)(当输入已经排序时)。