®
投球手
通常用于指示投球手的技能的指标是
- 经济(他们每次承认有多少次运行)
- 罢工率(每个检票口打保龄球)
- 平均(每个检票口承认)
我觉得这些指标已经足够好,可以指示投球手的类型。
经济衡量一个圆顶硬礼帽的跑步较少,而打击率衡量了投球手的检票口能力。
平均水平低意味着一个圆顶硬礼帽的经济和打击率统计数据。
我命名评分:
- 经济
- Wicket_taking_rating
- bowling_consistency_rating
这些将使用此公式进行标准化:
z=−σx−μ
x
is the data point in question.
μ
is the mean of the whole dataset
σ
is the standard deviation of the whole dataset
z
is the resulting score. It shows how many standard deviations above/below the average the datapoint is.
This is almost the same as the formula used for batting, except for the negation at the front. Since lower economies, strike rates and averages are better, the scores are negated so that a higher rating would indicate a more skilled bowler.
I also decided to use another rating:
- specialist_rating
- used to measure whether a bowler is a specialist, part-timer or a non-bowler
- Number of balls bowled / number of matches played
This rating will be standardised using the original standardisation formula.
经验
目前,一名职业生涯中只面对4个球,在大多数击球等级中都获得了很高的数字。显然,情况并非如此,因为裁员将无法在很长一段时间内保持这些数字。同样,击球手在职业生涯中可能打了几次不错的球,最终可能比一些既定的投球手要高。
因此,需要调整这些评分以说明他们作为击球手和投球手的经验。
球员击中的局数将决定击球体验。
球员保龄球的球数将决定保龄球的经历。
这两个都将是标准化的(使用以前的公式),它们的值将从-1.5到1.5,这样评分不仅仅是喜欢玩过最多的玩家。
。
一旦标准化,每个播放器等级将被调整如下:
- 如果评分是击球等级,请在评分中添加击球体验。否则,添加保龄球经验。
- 重新标准这个新号码
探索评分
我编写了一个脚本,可以从数据集中浏览每个球,并计算播放器的整体评分并将其保存到CSV文件中。您可以看到下面数据的片段。

根据这些评分...
IPL中排名前15位最快的得分手是:
- pn mankad
- 广告罗素
- v sehwag
- AB de Villiers
- GJ Maxwell
- rr pant
- ch gayle
- ka polard
- HH Pandya
- Spar Narine
- yk pathan
- DA Warner
- SR Watson
- sa yadav
- DA Miller
前15名最一致的击球手:
- iqbal abdulla
- kl rahul
- DA Warner
- AB de Villiers
- ch gayle
- MS Dhoni
- DA Miller
- v kohli
- rr pant
- f du plessis
- JC Buttler
- S Dhawan
- JP Duminy
- SPD Smith
- SK Raina
排名前15位的爆炸性击球手(在边界中得分的最高比例):
- pn mankad
- B Stanlake
- rs sodhi
- v sehwag
- Spar Narine
- 广告罗素
- ch gayle
- GJ Maxwell
- SR Watson
- rr pant
- AB de Villiers
- sa yadav
- BB McClum
- 史密斯博士
- DA Warner
前15名完成者:
- ra jadeja
- HH Pandya
- DJ Bravo
- MS Dhoni
- DA Miller
- Harbhajan Singh
- Jr Hazlewood
- yk pathan
- ik pathan
- iqbal abdulla
- Mukesh Choudhary
- p sau
- ba bhatt
- k upadhyay
- 是泰勒
前15名最艰难的跑步者(非边界评分的跑步比例最高):
- CRD Fernando
- DP Vijaykumar
- NJ Rimmington
- rg更多
- SPD Smith
- DA Miller
- ra jadeja
- v kohli
- AB de Villiers
- MS Dhoni
- MP Pandy
- arpatel
- 在Rayudu
- kl rahul
- SK Raina
最经济的15个最经济的投球手:
- 广告罗素
- sn takur
- GJ Maxwell
- SR Watson
- pp chawla
- 我莫克尔
- JJ Bumrah
- Str Binny
- DL Chahar
- HV Patel
- 拉希德·汗(Rashid Khan)
- Mohammed Siraj
- R Vinay Kumar
- kh pandya
- k rabada
前15名最佳检票口:
- Sandeep Sharma
- RP Singh
- MM Patel
- ut yadav
- GJ Maxwell
- mg johlin
- 拉希德·汗(Rashid Khan)
- arpatel
- nehra
- sn takur
- MM Sharma
- AB Dinda
- JD Unadkat
- DL Chahar
- DJ Bravo
前15个最一致的投球手:
- MM Patel
- Sandeep Sharma
- RP Singh
- nehra
- mg johlin
- ut yadav
- arpatel
- AB Dinda
- 拉希德·汗(Rashid Khan)
- GJ Maxwell
- JH Kallis
- MM Sharma
- Harbhajan Singh
- r bhatia
- sn takur
显然,每个评分中都有一些异常情况,尽管有经验纠正经验,但一些保龄球的排名高于专家击球手。但是,这些异常的玩家并没有将其他评级延续到其他评级,整个评分确实很有意义。
匹配数据
对于每个球,以及玩家技能数据,还将考虑当前比赛的上下文。
每个球将考虑以下信息:
- 球号
- 击球手得分
- 击球手面对的球
- 击球手面对的球的比例,导致0跑
- 击球手面对的球的比例,导致1跑
- 击球手面对的球的比例,导致2次奔跑
- 击球手面对的球的比例,导致3次奔跑
- 击球手面对的球的比例,导致4次奔跑
- 击球手面对的球的比例,导致6次奔跑
- 投球手承认
- 投球手打保龄球的球数
- 投球手摄取的检票口
- 由投球手打保龄球的球的比例
- 由投球手打保龄球的球的比例
- 由投球手打保龄球的球的比例
- 由投球手打保龄球的球的比例
- 由投球手打保龄球的球的比例
- 由投球手打保龄球的球的比例
- 圆顶硬礼帽的球的比例
- 追逐分数(如果适用)
- 所需的运行率(如果适用)
- 局得分
- 局门
所有这些都将按照之前的标准化。
构建数据集
现在已经确定要使用的数据了,该是时候将球CSV文件处理到数据集中进行训练。
import pandas as pd
import numpy as np
import os
import pickle as pkl
# standardising formula
def zscore(col):
mean = col.mean()
std = col.std()
return (col - mean) / std
df = pd.DataFrame() # will hold the final dataset at the end
player_db = pd.read_csv("player-db.csv") # need it for player ratings
下面的代码通过每场匹配,并将相关数据添加到数据框中。
for file in os.listdir("matches"):
f = os.path.join("matches", file)
match_df = pd.read_csv(f)
match_df = match_df.fillna(0)
# columns of all the match data needed
ball_no = []
striker = []
bowler = []
batsman_runs = []
batsman_balls = []
batsman_outcome_dists = { outcome : [] for outcome in [0,1,2,3,4,6]}
bowler_economy = []
wicket_taking = []
bowler_consistency = []
bowler_wickets = []
bowler_runs = []
bowler_balls = []
bowler_outcome_dists = { outcome : [] for outcome in range(0, 7) }
innings_score = []
innings_wickets = []
chasing = []
req_run_rate = []
outcome = []
batsmen = {}
bowlers = {}
score = 0
wickets = 0
chasing_score = 0
prev_innings = 1
for ball in match_df.iloc:
batter = ball["striker"]
_bowler = ball["bowler"]
striker.append(batter)
bowler.append(_bowler)
runs = int(ball["runs_off_bat"])
runs = min(runs, 6)
runs = 4 if runs == 5 else runs
wides = int(ball["wides"])
wicket = 1 if ball["wicket_type"] else 0
innings = int(ball["innings"])
if innings != prev_innings:
chasing_score = score
score = 0
wickets = 0
prev_innings = innings
if batter not in batsmen:
# this will hold the number of balls faced for each outcome by a batsman
batsmen[batter] = {
0: 0,
1: 0,
2: 0,
3: 0,
4: 0,
6: 0
}
if _bowler not in bowlers:
# this will hold the number of balls bowled for each outcome by a bowler (5 means wicket)
bowlers[_bowler] = {
0: 0,
1: 0,
2: 0,
3: 0,
4: 0,
5: 0,
6: 0
}
## Batting Data ##
batsman_balls_faced = np.sum([batsmen[batter][i] for i in batsmen[batter]])
batsman_dist = { _outcome : 0 if batsman_balls_faced == 0 else batsmen[batter][_outcome] / batsman_balls_faced for _outcome in batsmen[batter]} # getting proportion of balls faced for each outcome
batsman_runs_scored = np.sum([_outcome * batsmen[batter][_outcome] for _outcome in batsmen[batter]])
for _outcome in batsman_outcome_dists:
batsman_outcome_dists[_outcome].append(batsman_dist[_outcome])
batsman_runs.append(batsman_runs_scored)
batsman_balls.append(batsman_balls_faced)
## Bowling Data ##
bowler_balls_bowled = np.sum([bowlers[_bowler][i] for i in bowlers[_bowler]])
bowler_runs_given = np.sum([_outcome * bowlers[_bowler][_outcome] if _outcome != 5 else 0 for _outcome in bowlers[_bowler]])
bowler_wickets_taken = bowlers[_bowler][5]
bowler_dist = { _outcome : bowlers[_bowler][_outcome] / bowler_balls_bowled if bowler_balls_bowled != 0 else 0 for _outcome in bowlers[_bowler] } # getting proportion of balls bowled for each outcome
for _outcome in bowler_outcome_dists:
bowler_outcome_dists[_outcome].append(bowler_dist[_outcome])
bowler_runs.append(bowler_runs_given)
bowler_wickets.append(bowler_wickets_taken)
bowler_balls.append(bowler_balls_bowled)
## Innings Data
innings_score.append(score)
innings_wickets.append(wickets)
chasing.append(chasing_score)
ball_outcome = runs if wicket == 0 else 5
outcome.append(ball_outcome)
discrete_ball_no = ball["ball"]
discrete_ball_no = int(discrete_ball_no) * 6 + round(discrete_ball_no % 1) * 10
ball_no.append(discrete_ball_no)
rem_balls = 120 - (discrete_ball_no - 1) if discrete_ball_no <= 120 else int(discrete_ball_no - 120)
_req_run_rate = max(0, (chasing_score - score) / rem_balls)
req_run_rate.append(_req_run_rate)
## Update State ##
batsmen[batter][runs] += 1
bowlers[_bowler][runs] += 1
bowlers[_bowler][5] += wicket
score += runs
wickets += wicket
new_match_df = pd.DataFrame()
new_match_df["striker"] = striker
new_match_df["bowler"] = bowler
new_match_df["batsman_runs"] = batsman_runs
new_match_df["batsman_balls"] = batsman_balls
for _outcome in batsman_outcome_dists:
new_match_df[f"batsman_{_outcome}"] = batsman_outcome_dists[_outcome]
new_match_df["bowler_runs"] = bowler_runs
new_match_df["bowler_balls"] = bowler_balls
new_match_df["bowler_wickets"] = bowler_wickets
for _outcome in bowler_outcome_dists:
new_match_df[f"bowler_{_outcome}"] = bowler_outcome_dists[_outcome]
new_match_df["innings_score"] = innings_score
new_match_df["innings_wickets"] = innings_wickets
new_match_df["ball"] = ball_no
new_match_df["chasing"] = chasing
new_match_df["req_run_rate"] = req_run_rate
new_match_df["outcome"] = outcome
frames = [df, new_match_df]
df = pd.concat(frames)
# df now contains the relevant match data from every single ball in the dataset
现在,这将播放器评级添加到收集的数据并保存数据集中。
batting_ratings = player_db[["player", "explosivity_rating", "consistency_rating", "finisher_rating", "quick_scorer_rating", "running_rating"]]
bowling_ratings = player_db[["player", "economy_rating", "wicket_taking_rating", "bowling_consistency_rating", "specialist_rating"]]
df = df.join(batting_ratings.set_index("player"), on="striker") # add batsmen's batting ratings to dataframe
df = df.join(bowling_ratings.set_index("player"), on="bowler") # add bowler's bowling ratings to dataframe
df = df.drop(["striker", "bowler"], axis=1) # remove the striker and bowler columns since they are not part of the features needed to predict the outcome of a ball
# get the means and standard deviations of each column
df_mean = df.drop(["outcome"], axis=1).mean()
df_std = df.drop(["outcome"], axis=1).std()
# save the mean and std of all the columns. this would be needed later for preprocessing when predicting new data.
with open("mean-std.bin","wb") as f:
pkl.dump({
"mean": df_mean,
"std": df_std
}, f)
# standardise all the columns except the ratings and outcome
for col in df.columns:
if col != "outcome" and "rating" not in col:
df[col] = zscore(df[col])
# shuffle
df = df.sample(frac=1)
# split into a training set and a testing set
training_split = int(len(df) * 0.85) # take 85% to train
training_df = df[:training_split]
testing_df = df[training_split:]
# save the datasets
training_df.to_csv("balls-train.csv", index=False)
testing_df.to_csv("balls-test.csv", index=False)
数据集看起来像这样。

培训和测试模型
我选择使用随机的森林分类器来训练数据,这确实很简单,快速使用Sklearn训练。
import numpy as np
import pandas as pd
from sklearn.ensemble import RandomForestClassifier
import pickle as pkl
from random import choices
dataset = pd.read_csv("balls-train.csv")
x = dataset.drop(["outcome"], axis=1)
y = dataset["outcome"]
clf = RandomForestClassifier(max_depth=15, n_estimators=50)
clf.fit(x, y)
with open("clf.bin", "wb") as f:
pkl.dump(clf, f)
现在要测试此模型,我们可以在测试集上看到其准确性。
test = pd.read_csv("balls-test.csv")
predicted = clf.predict(test.drop(["outcome"], axis=1))
print (np.sum(predicted == test["outcome"]) / len(test))
在以下输出中运行此结果:
44%的精度似乎并不太好。但是,每个球都可以很容易地具有2或3个合理的结果,因此使用精度不是捕获模型表现方式的好方法。
相反,我认为最好查看每个结果的输入数据。对于每个结果,以模型预测具有此结果的输入,并将测试集中标记为该结果标记的输入。如果输入上的这两组相似,则该模型可以很好地预测此结果。
test = pd.read_csv("balls-test.csv")
predicted = test.drop(["outcome"], axis=1)
preds = clf.predict(predicted)
predicted["outcome"] = preds
for outcome in range(0, 7):
print ("Outcome ", outcome)
# get rows which were labelled with this outcome in the test data
test_slice = test[test["outcome"] == outcome]
# get rows which were predicted with this outcome by the model
predicted_slice = predicted[predicted["outcome"] == outcome]
# a vector of the average values of the inputs that were labelled with the outcome in the test set
test_slice_mean = test_slice.mean()
# a vector of the average values of the inputs that were predicted to have this outcome by the model
predicted_slice_mean = predicted_slice.mean().fillna(0)
# calculates the euclidean distance between the two vectors
dist = ((predicted_slice_mean - test_slice_mean) ** 2).sum() ** 0.5
print ("Actual Count", len(test_slice), "Predicted Count", len(predicted_slice)) # compared how many times this outcome appeared in the test set and how many times it got predicted
print ("Average Distance", dist)
运行此过程会导致以下输出...
Outcome 0
Actual Count 12041 Predicted Count 13324
Average Distance 1.1953108714619187
Outcome 1
Actual Count 12564 Predicted Count 20402
Average Distance 0.8442394082114827
Outcome 2
Actual Count 2055 Predicted Count 16
Average Distance 4.355749118524852
Outcome 3
Actual Count 112 Predicted Count 0
Average Distance 4.526265034977223
Outcome 4
Actual Count 3848 Predicted Count 74
Average Distance 2.6306944519746605
Outcome 5
Actual Count 1646 Predicted Count 20
Average Distance 3.586353351892623
Outcome 6
Actual Count 1628 Predicted Count 58
Average Distance 4.243057588990431
这表明该模型的性能差。考虑到输入中值的幅度,它的距离对于每个结果的距离都很大。
它也无法匹配测试集中的结果比例,预测计数与实际计数非常不同。
对于每个球,该模型显然偏向于预测0和1。这确实是有道理的,因为这些是板球游戏中最常见的结果。
这里的问题是如何做出预测。该模型输出每个球的结果的概率分布。目前,以最高概率的结果为预测的结果。随机选择结果,使用概率分布来加权随机选择会更有意义。
这是相同的代码,但使用加权随机选择。
test = pd.read_csv("balls-test.csv")
predicted = clf.predict_proba(test.drop(["outcome"], axis=1))
preds = []
for weights in predicted:
outcomes = [0,1,2,3,4,5,6]
# weighted random selection
p = choices(outcomes, weights=weights)
preds.append(p[0])
predicted = test.drop(["outcome"], axis=1)
predicted["outcome"] = preds
for outcome in range(0, 7):
print ("Outcome ", outcome)
test_slice = test[test["outcome"] == outcome]
predicted_slice = predicted[predicted["outcome"] == outcome]
# a vector of the average values of the inputs that were labelled with the outcome in the test set
test_slice_mean = test_slice.mean()
# a vector of the average values of the inputs that were predicted to have this outcome by the model
predicted_slice_mean = predicted_slice.mean().fillna(0)
# calculates the euclidean distance between the two vectors
dist = ((predicted_slice_mean - test_slice_mean) ** 2).sum() ** 0.5
print ("Actual Count", len(test_slice), "Predicted Count", len(predicted_slice))
print ("Average Distance", dist)
运行此结果在以下结果...
Outcome 0
Actual Count 12041 Predicted Count 12072
Average Distance 0.06285163994309419
Outcome 1
Actual Count 12564 Predicted Count 12507
Average Distance 0.047105551432281484
Outcome 2
Actual Count 2055 Predicted Count 2089
Average Distance 0.13890305459997243
Outcome 3
Actual Count 112 Predicted Count 94
Average Distance 0.779151006384056
Outcome 4
Actual Count 3848 Predicted Count 3858
Average Distance 0.09621869495553977
Outcome 5
Actual Count 1646 Predicted Count 1676
Average Distance 0.2084278773037825
Outcome 6
Actual Count 1628 Predicted Count 1598
Average Distance 0.29624599526308754
现在可以看到模型的性能很好。它与测试集的结果比例相匹配,并且输入之间的距离已减少到很小的范围。
探索每个功能
我认为看到数据集的每个功能有助于球的结果是很有趣的。
如下所示是每个功能的框图,相对于每个预测结果,以帮助可视化每个输出的特征分布。这将有助于展示功能如何促进结果。
击球手的奔跑

击球手的球

击球手的点球比例

击球手的单比例
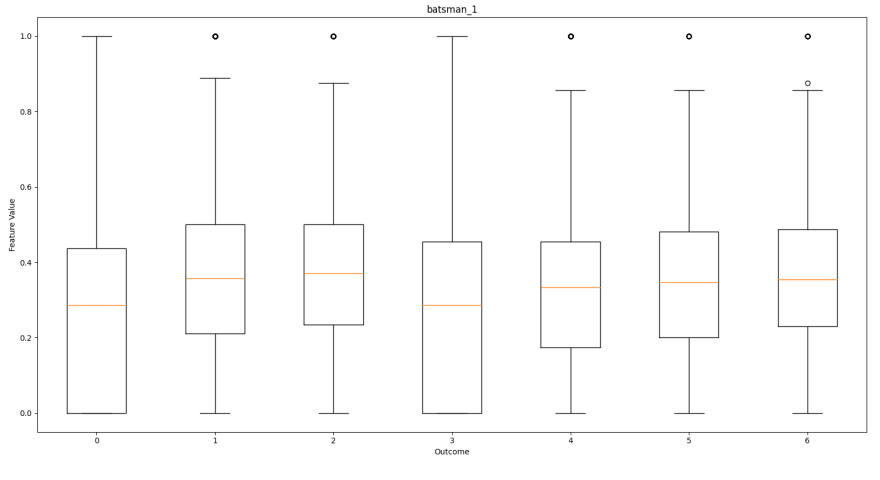
击球手的双重比例

击球手的三跑比例

击球手的四跑比例

击球手的六跑比例

投球手承认

投球手打保龄球的球数

投球手拿走的小门

投球手的点球比例

鲍勒的单比例

鲍勒的双重比例

鲍勒的三跑比例

鲍勒的四跑比例
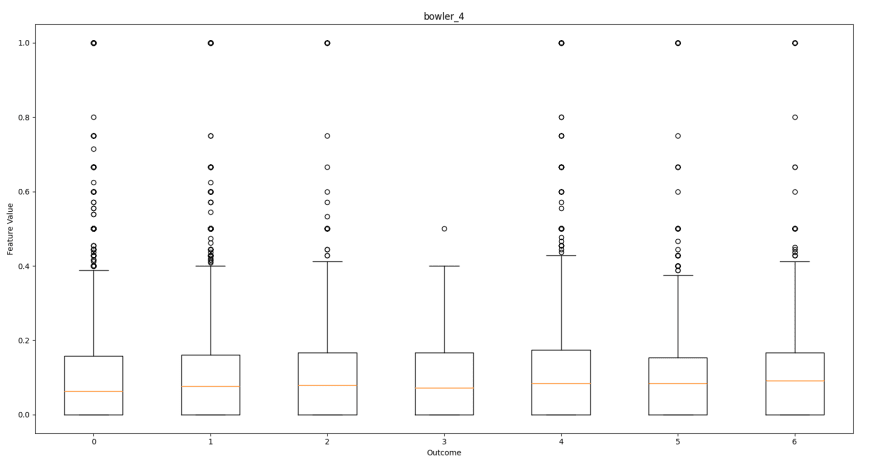
投票台的检票口送货比例

鲍勒的六跑比例

局得分
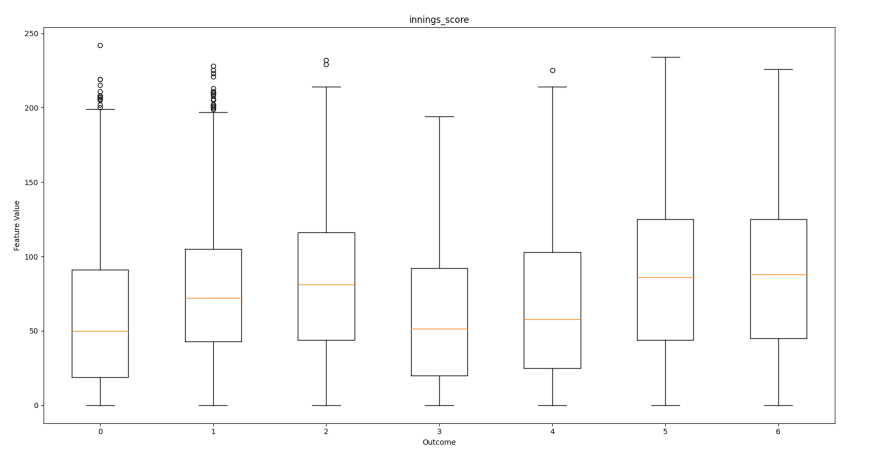
局门
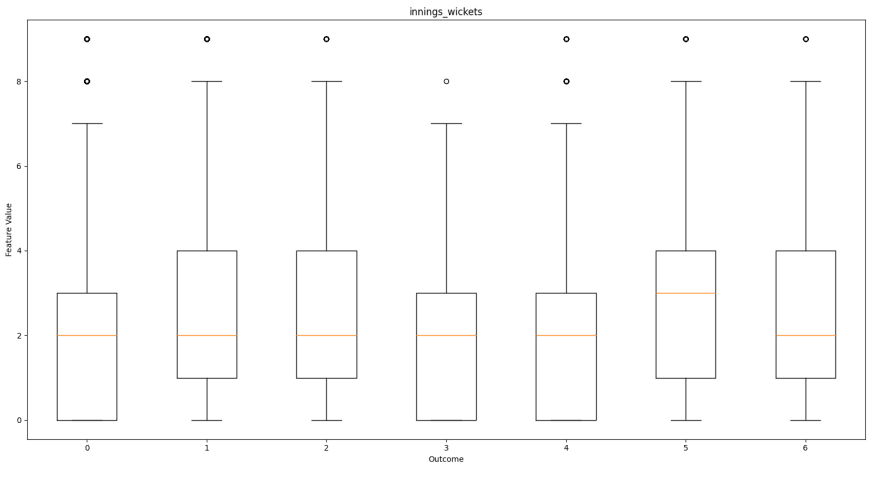
局的球号

得分为追逐

所需的运行率

爆炸性等级

一致性等级

终结器评级

快速得分手评级

运行等级
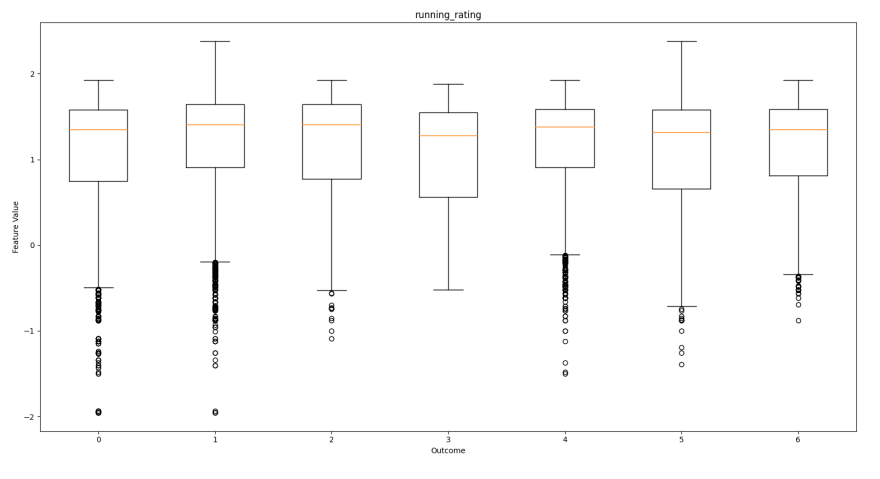
经济评级

检票口评级

保龄球一致性评级

保龄球专家评级

从这些框图中,我们可以看到哪些功能对结果有更多影响。
为每个结果产生相似外观盒子的特征对球的结果没有太大影响。这些功能包括:
- 击球手/圆顶球结果比例
- 投球手评级
- 投球手摄取的检票口
- 追逐得分
- 要求运行率
看到追逐得分和所需的运行率特征对结果没有太大影响并不奇怪,因为数据集中的一半球不会应用这些功能。
看到球结果比例也不奇怪。此列表中的检票口也具有功能。这是因为它们具有相同的值在整个板球比赛中都出现相同的值,因此它们必然会具有相同值的各种结果。
我很惊讶地看到,在击球等级的情况下,鲍勒评分对结果没有太大影响。
这可能意味着几件事
- 比赛的结果更归结于球队的击球阵容强大而不是打保龄球。
- 必须有一种更好的方法来量化投球手的技能
考虑到这一点,虽然我确实认为这是两者的混合,但我觉得这主要是由于第一点。
我相信这是因为,尤其是在像IPL这样的比赛中,投球手的质量并不像板球运动员那样波动(至少从统计学上讲)。让投球手 /非专业板球运动员参加比赛更为普遍,虽然您几乎永远不会在比赛中找到击球手打保龄球,偶尔会找到兼职的投球手。< / p>
量化投球手技能的方法仍然可以提高,但可能考虑以下一些:
- 投球手的平均速度
- 圆顶硬礼帽的平均转弯程度(用于旋转器)
- 调整他们的经济/检票口采取评分以考虑他们在
中的比赛的背景
这些数据不在我拥有的数据集的范围之内,但将来可以实施改进该项目。
尽管如此,我对模型的训练方式感到满意,与测试数据集紧密保持一致。
第2部分
为避免使这一部分太长,我决定将其分为两个部分。
第2部分将涉及构建实际的匹配模拟器。我将使用它来查看它在模拟真实游戏中的作用,并回答有关任何假设游戏情况的任何问题。
谢谢您的阅读!
