Advent of Code deste ano的第三天，讨论数据结构操作的复杂性非常有趣。

第三天的问题

第3天"reorganização da mochila"的问题是在不同的值集合中找到重复的元素。同样，我建议您先尝试解决它，而Vanido do Bruno Rocha：

问题 - 数据结构和操作的复杂性

一种非常简单的方法来表示上半场背包隔间，或下半年的背包，它是列表或数组，每个位置都是项目。这很简单明了，已经使许多语言允许您访问字符串位置的字符，从而使字符串以某种方式表现得像列表。

在两个字符串中找到共同的项目只会比较其所有元素。示例：

itens_em_comum = []
for a in compartimento1:
    for b in compartimento2:
        if a == b:
            itens_em_comum.append(a)

这仍然可以简化以下内容：

for a in compartimento1:
    if a in compartimento2:
        itens_em_comum.append(a)

从更改中apense，方法将执行完全相同的步骤，将其与每个koud1项目与每个koud0项目进行比较。这使得n * m比较是n，是koud0和m中的物品数量的Koud1中的项目数量，而Koud1中的项目数量与第1部分中的两个隔间相同（Koud7），©可以说他们可以说他们可以说他们可以说。是n²比较（O(n²)）。

色情©m列表不是可以代表隔室的数据结构。由于此问题在同一隔间中重复项目，并且其顺序并不重要，因此可以使用集合（在某些编程语言中称为 sep ），并且可以使用árvore de busca binária或tabela de espalhamento实现。示例：

compartimento2 = set(compartimento2)
for a in compartimento1:
    if a in compartimento2:
        itens_em_comum.append(a)

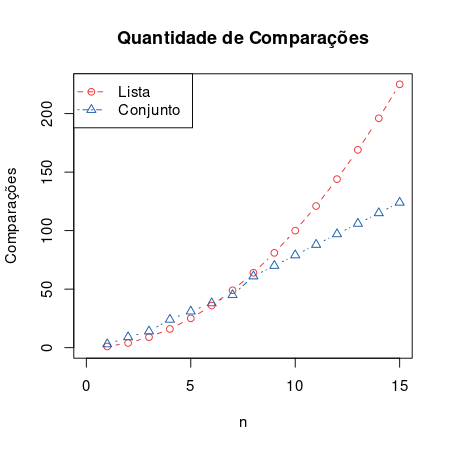
使用集合的一个优点是删除了重复的项目，即与同一项目的另一个高度没有进行相同的比较。另一个优点是，在搜索量中实施时，验证另一个项目是否存在于另一组中的操作将搜索空间减少一半，每次比较£，因此大约n * log2(n)比较以查找所有重复的项目，该项目小于n²8 。

然而，在列表中，要添加一个项目，只需在其末尾复制它（O(1)），就需要在双子搜索件中添加一个项目才能在河中找到该物品的位置£o（O(log2(n))） ），这是每个项目都重复的，有时有必要反叛裁决。简而言之，有一些处理以建造树，必须考虑这一点。一部分以来，由于河流的建设与后来发生的搜索的复杂性相同（O(n * log2(n))），因此它补偿了大量物品，但不能补偿低量案例。

考虑

相同的操作对于不同的数据结构可能具有不同的复杂性，因为在这种情况下，验证另一个集合中是否存在一个项目（列表中的Koud9和O(n * log2(n))集）。手术的pord©m，可能有必要考虑构建数据结构，在这种情况下，该结构弥补了许多项目，但可能无法补偿少量。P> p>

还有其他选择可以解决此问题，例如将两个隔室转换为集合并使用寻求其interseção的功能（由Bruno Rocha在其Vares中完成）。这需要构造另一组，如果算法不利用此数据结构，例如旅行集合的项目是否存在，这是使用一个隔间的列表和一组的列表发生的情况另一方面，这不能改变算法的循环复杂性，并使较慢。

©m在使用Abiaqian7实现集合时（Python做到这一点）时，还可以分析复杂性，这将为这些操作带来另一种复杂性，并且可以或不再工作，如dia 2所述，可以更好地工作，如所讨论的。

，甚至可以使用列表，可以订购这些项目，这将允许列表中的busca binária（我推荐此vídeo sobre o assunto），这不会删除重复处理项目，因为BAMINARY SEERCH的订单和O(log2(n))将会具有类似于分析的其他选项的算法的效率（O(n * log2(n))）。