深度搜索二进制树-DEV365 开发者社区

在此previous blog post中，我们了解了二进制树是什么，如何表示它以及不同类型的二进制树，总而言之，我们说，与其他数据结构不同，二进制树可以浏览两种不同的方式呼吸优先搜索和深度优先搜索。

这篇文章将重点放在深度优先搜索上。

什么是深度优先的搜索树遍历

深度优先搜索是一种算法，使您可以穿越整棵树。逻辑是，您一直向前前进，直到到达叶子（一个没有左或右子的节点），然后根据您使用的方法回溯。

深度优先的搜索树可以以三种方式写入：预订，顺序和oder后遍历。可以递归和迭代地编写每种方式。您选择的方式会影响结果。让我向您展示区别：

预购

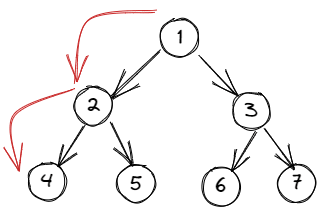
提示在名称，预订，当您编写预订遍历时，您可以访问父节点，然后访问左边的孩子。如果您使用预订方法遍历上面的树，则结果应为：

让我们用JavaScript编写递归和迭代实现

递归

function dfsPreOrderRecursive(node, arr = []){
  if(node){
    arr.push(node.val); 
    if(node.left) dfsPreOrderRecursive(node.left, arr);
    if(node.right) dfsPreOrderRecursive(node.right, arr);
  }
}

说明，由于您知道要访问节点的顺序，因此递归方法大多是简单的。在这里，我们必须访问父节点，然后访问其孩子。因此，我们将当前节点的值推入结果数组，然后检查其是否具有左或右子，如果是这样，我们通过给子节点和结果数组来调用该功能。

迭代

function dfsPreOrderIterative(root){
  const stack = [root]
  const result = []; 
  let current;

  while(stack.length){
    current = stack.pop(); 
    result.push(current.val);

    if(current.right) stack.push(current.right); 
    if(current.left) stack.push(current.left); 
  }

  return result; 

  }

解释：如果没有任何约束，则预先遍历是直接的方法。由于我们不需要检查节点是否有任何孩子，因此我们将当前节点的值推到结果，然后检查其是否有孩子，如果这样，它们将被添加到堆栈中。由于我们使用的是堆栈，我们将右向左推右，并且遵循FIFO订单。

为了

对于订购遍历，您必须在回溯到父母和正确的孩子之前访问左孩子。当您当前的节点有一个左孩子时，您必须继续前进。如果您使用订购方法遍历上面的树，则结果应为：

让我们用JavaScript编写递归和迭代实现。

递归

function dfsInOrderRecursive(node, arr = []){ 
  if(node){
    if(node.left) dfsInOrderRecursive(node.left, arr);
    arr.push(node.val); 
    if(node.right) dfsInOrderRecursive(node.right, arr);
  }

  return arr; 

 }

说明：由于您知道要访问节点的顺序，因此递归方法大多是简单的。在这里，我们必须在回溯到父母之前访问左孩子，然后访问右子女，因此我们检查当前的节点是否有左孩子，如果是，我们通过给孩子来调用该功能s值进入结果数组，最后我们检查是否存在合适的孩子，如果是这样，我们通过给合适的孩子来调用该功能。

迭代

function dfsInOrderIterative(root){
  const stack = []; 
  const result = [];
  let current = root; 

  while(stack.length || current){
    while(current){
      stack.push(current); 
      current = current.left; 
    }
    current = stack.pop();
    result.push(current.val); 
    current = current.right;
  }

  return result;
}

说明： 对于阶段遍历，我们必须推动左子女，父母，然后推动右子。这意味着我们必须从剩下的孩子开始前进。对于迭代实现，当前循环浏览所有左子女，然后如果没有左子女，则将当前节点的值推入结果。

邮寄订单

对于后订单遍历，您必须在回溯到父母之前访问孩子。您必须在当前节点有孩子的同时继续前进。如果您使用后订单方法遍历上面的树，则结果应为：

让我们用JavaScript编写递归和迭代实现。

递归

function dfsPostOrderRecursive(node, arr = []){
  if(node){
    if(node.left) dfsPostOrderRecursive(node.left, arr);
    if(node.right) dfsPostOrderRecursive(node.right, arr);
    arr.push(node.val);
  }

  return arr;
}

说明：由于您知道要访问节点的顺序，因此递归方法大多是简单的。在这里，我们必须在父母面前访问孩子，因此我们检查当前节点是否有左或右子孩子，如果是，我们通过给孩子来调用该功能，然后将值推入结果数组中。

迭代

function dfsPostOrderIterative(root){
  const s1 = [root];
  const s2 = [];
  const result = []; 
  let current;

  while(s1.length){
    current = s1.pop();

    if(current.left) s1.push(current.left);
    if(current.right) s1.push(current.right);

    s2.push(current.val);
  }

  return s2.reverse();

}

复杂性分析

我们在这篇文章中看到的每种方法都具有相同的时间和空间复杂性o（n）甚至递归方法，因为每个递归功能都使用引擎盖下的堆栈，以跟踪您正在穿越的元素。您的选择将取决于您必须解决的问题。