神经网络中的重量初始化技术
#python #machinelearning #deeplearning

为什么要重量初始化？

重量初始化的主要目的是防止层激活输出在正向传播过程中爆炸或消失的梯度。

现在，我们想到了为什么消失的梯度下降问题出现：

当我们在梯度下降中找到基本上是斜率的衍生术语时，如果图层增加，权重更新将不会受到巨大差异的影响（Sigmoid函数的衍生范围在0到0.25之间） 。

如果出现上述问题，损失梯度要么太大或太小，而且网络甚至可以这样做，将需要更多时间来收敛。
如果我们正确初始化了权重，那么我们的目标即将在最少的时间内实现损失函数的优化，否则使用梯度下降将融合到最小值。

重量初始化的关键点：

1）重量应该很小：

神经网络中的较小权重可能会导致模型更稳定且不太可能过度拟合训练数据集，从而在对新数据进行预测时具有更好的性能。

2）重量不应相同：

如果将所有权重初始化为零，则所有层的所有神经元都执行相同的计算，通过使整个深网无用，从而给出相同的输出。如果权重为零，那么整个深网的复杂性将与单个神经元的复杂性相同，并且预测无非是随机的。它可能导致死亡神经元的情况。

在连接到同一输入的隐藏层中并排并排的

节点必须具有不同的权重以更新权重。
通过将权重作为非零（但接近0（例如0.1）等），该算法将在接下来的迭代中学习权重，并且不会被卡住。这样，打破对称性就发生了。

3）权重应具有良好的差异：

重量应该具有良好的差异，以便网络中的每个神经元应以不同的方式行为，以避免任何消失的梯度问题。

重要的重量初始化技术：

在进行技术之前，我们将定义两个表达式：

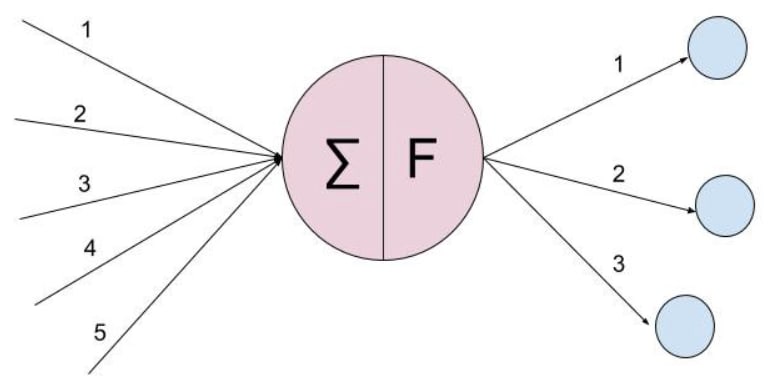
fan_in ：神经元的输入数
fan_out ：神经元的输出数

Weight Initialization

在上图中，fan_in = 5，fan_out = 3

现在可以出现这个问题，就像我们应该只服用fan_in和fan_out来定义输入数量和输出数？

答案是否定的，您可以定义您选择的任何表达式。对于研究人员使用的说明。

1）均匀分布：

均匀分布是从均匀分布中随机初始化权重的一种方式。它告诉我们可以初始化遵循最小值和最大值的统一分布标准的权重。它对Sigmoid激活函数效果很好。<<<<<<<<<<<< /p>

重量计算将是：

我们〜d [-1 / sqrt（fan_in），1 / sqrt（fan_in）] < / p>

其中d是统一分布
代码：

import keras
from keras.models import Sequential
from keras.layers import Dense
#Initializing the ANN
classifier=Sequential()
#Adding the NN Layer
classifier.add(Dense(units=6,activation='relu'))
classifier.add(Dense(units=1,kernel_initializer='RandomUniform',activation='sigmoid'))
# Summarize the loss
plt.plot(model_history.history['loss'])
plt.plot(model_history.history['val_loss'])
plt.title('model_loss')
plt.xlabel('epochs')
plt.ylabel('loss')
plt.legend(['train','test'],loc='upper left')
plt.show()

py

这里kernel_initializer是随机分辨

时期与损失函数图：

Loss function

2）Xavier/Glorot初始化：

Xavier初始化是一种高斯初始化启发式，可将输入的方差保持在与层输出相同的层相同的层。这确保了整个网络中的方差保持不变。它适用于Sigmoid函数，并且比上述方法更好。在此类型中，有两个变体：

i）Xavier正常：

平均值= 0
的正态分布 我们〜n（0，std）其中std = sqrt（2 /（fan_in + fan_out）< / p>

这里n是一个普通方程。

ii）Xavier制服：

我们〜d [-sqrt（6） / sqrt（fan_in + fan_out），sqrt（6） / sqrt（fan_in + fan_out）] < / p>

其中d是统一分布

代码：

import keras
from keras.models import Sequential
from keras.layers import Dense
#Initializing the ANN
classifier=Sequential()
#Adding the NN Layer
classifier.add(Dense(units=6,activation='relu'))
classifier.add(Dense(units=1,kernel_initializer='glorot_uniform',activation='sigmoid'))
# Summarize the loss
plt.plot(model_history.history['loss'])
plt.plot(model_history.history['val_loss'])
plt.title('model_loss')
plt.xlabel('epochs')
plt.ylabel('loss')
plt.legend(['train','test'],loc='upper left')
plt.show()

py

这里的kernel_initializer是glorot_uniform/glorot_normal

时期与损失函数图：

Loss Function

3）他init：

此权重初始化也有两个变化。它适用于Relu和LeakyRelu激活功能。

i）他正常：

平均值= 0
的正态分布 wij〜n（平均，std），平均值= 0，std = sqrt（2/fan_in）

其中n是正态分布

ii）他统一：

我们〜d [-sqrt（6 / fan_in），sqrt（6 / fan_in）] < / p>

其中d是统一分布

代码：

#Building the model
import tensorflow as tf
import keras
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import PReLU,LeakyReLU,ELU
from keras.layers import Dropout
#Initializing the ANN
classifier=Sequential()
#Adding the input Layer and the first hidden Layer
classifier.add(Dense(units=6,kernel_initializer='he_uniform',activation='relu',input_dim=11))
classifier.add(Dense(units=6,kernel_initializer='he_uniform',activation='relu'))
classifier.add(Dense(units=1,kernel_initializer='glorot_uniform',activation='sigmoid'))
classifier.compile(optimizer='adam',loss='binary_crossentropy',metrics=['accuracy'])
y_pred=classifier.predict(X_test)
y_pred=(y_pred>0.5)

py
这里的kernel_initializer是he_uniform/he_normal

我们得出结论。当我处理搅动建模问题时，我尝试了上述权重初始化技术，并能够找到哪种技术最适合每个激活功能，例如relu，sigmoid.i已将数据集附加了您的参考Churn Modelling dataset

重量初始化技术不限于上述三个。但是上述三种方法已被研究人员广泛使用。