欢迎大家进入我教AI如何降落在月球上的帖子。
当然,我不是在谈论实际的月亮(尽管我希望自己是)。但是,我谈论的是模拟环境(Openai的Lunar Lander健身房环境)
强化学习
我最近遇到了一篇有关DeepMind的Alphatensor的文章。
您可以阅读here
alphatensor学会了如何以极其有效的方式将两个矩阵乘以两个矩阵,以比Strassen的算法(以前的最佳算法)以更少的步骤完成乘法。
。阅读本文启发了我阅读我对我不太了解的机器学习领域 - 强化学习。 DeepMind建造了其他几个非常令人印象深刻的AI,它们都是使用强化学习算法训练的。
什么是强化学习?
强化学习涉及学习在环境中某些情况下采取的最佳行动,以实现某个目标。例如,在国际象棋游戏中,RL算法将学习移动什么以及在何处移动它,鉴于游戏板的状态和赢得游戏的目标。
rl模型纯粹从它们在环境中的互动中学习。在给定情况下,他们没有给予他们最佳采取的培训数据集。他们从经验中学习一切。
他们如何学习?
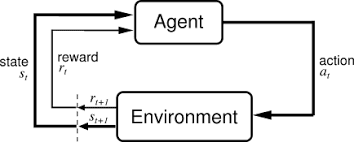
代理是与环境相互作用的任何事物通过观察并根据那些观察结果采取行动。
对于代理在环境中采取的每种动作,给定代理人的奖励,这表明了该动作的良好,鉴于环境中代理的目的和目的。
rl算法基本上通过反复试验改善了这些试剂的性能。他们最初执行随机操作,并查看他们从他们那里获得什么回报。然后,他们可以根据这些动作奖励对制定策略。一项政策描述了在给定情况下采取的最佳行动,并牢记环境的目标。
有几种算法可用于制定策略。
对于这个项目,我使用了DQN(深Q-Network)来制定策略。
Q值和DQN
dqns是在环境状态下作为输入和输出 q值输出的神经网络。它描述了代理商的政策。
没有针对DQN的固定模型体系结构。它因环境而异。例如,玩Atari游戏的代理商可能会通过游戏的图片观察环境。在这种情况下,最好将卷积层用作DQN体系结构的一部分。使用简单的前馈神经网络可以与其他环境(例如Openai's Gym的Lunar Lander环境)一起使用。
q值衡量预期的未来奖励在采取该行动时,假设将来遵循相同的政策。当代理遵循策略时,它采取了最大Q值的诉讼。
在我浏览代码时,将解释DQN的训练方式以确定准确的Q值。
当环境中的动作空间离散时,使用dqns,即代理在环境中可以采取的可能动作有限。
例如,如果涉及驾驶汽车的环境,则其动作空间将被视为离散如果唯一的动作是向前行驶,则左转和右转10度。如果涉及指定方向盘角度和行驶速度的动作,它的动作空间将是连续。这是因为它们可以采用无限数量的值,因此,有无限数量的动作。
问题和代码
正如我之前提到的,我将在Openai的Lunar Lander健身房环境中培训一名代理商。
在这种环境中,代理的目的是将着陆器降落在两个旗帜之间的腿上。
代理可以采取4个操作:
- 什么都不做
- 火左引擎
- 火右引擎
- 消防主引擎
从这种环境中获取的观察是一个8维矢量,包含:
- x坐标
- y坐标
- x速度
- y速度
- 着陆器的角度
- 角速度
- 2个布尔人描述每条腿是否与地面接触
代理人的奖励如下:
- 崩溃的-100点
- +100点休息
- +10点与地面接触
- -0.3分帧发射主引擎
- -0.03点发射侧引擎的每个帧
- +100-140点从顶部移到着陆垫
- 如果代理在一集中至少收集了200点,则认为该代理已解决了该环境。
情节 - 在满足环境重置的某些标准之前发生的一系列步骤/帧(情节终止)
情节终止于:
- 着陆器崩溃
- 着陆器水平脱颖而出
培训DQN
代理通过采取行动与环境互动。对于环境中的每个步骤,代理将以下记录为重播内存:
- 对环境的观察
- 从这个观察中采取的行动
- 获得的奖励
- 环境的新观察
- 该情节是否已终止
代理具有初始探索率,它决定了应进行随机移动的频率而不是从DQN的策略中采取行动。
这是为了在训练阶段探索所有动作,因此允许算法查看在某些情况下哪些动作最佳。 DQN的初始政策是随机的,因此,让代理商一直遵循它将意味着DQN将难以训练制定强大的政策,因为没有针对同一州探索不同的行动。
每发情节后,勘探率降低了适当的速度。到勘探率达到0时,代理人将仅遵循DQN的政策。到这个时候,DQN应该制定出强大的政策。
is the policy function. Takes in the environment state and an action as input and returns the q-value for that action.
is the current state
is a possible action
the reward for taking action at state
the state of the environment after taking action at state
is the action with the highest q-value at state
is the discount rate. It is a specified constant measuring how important future actions are in the environment.
For every n steps in the environment, a random batch is taken from the replay memory.
The DQN then predicts the q-values at each state in the batch and the q-values at each of the new states, so that the best action at that state can be obtained .
For each item in the batch, the calculated , and reward values are substituted into the equation above. This should calculate a slightly better value for this batch item.
The DQN is then trained with the batch observations as input and the newly calculated values as output.
Note: calculating
and the
values are done by separate networks - the policy and target network. They are initialised with the same weights. The policy network is the main network that is trained. The target network isn't trained, however the policy network's weights are copied to for some every m steps in the environment.
This is done so that the training process becomes stable. If one network was used to predict both
and
and trained, the network would end up be chasing a forever moving target, leading to poor results. The use of the target network to calculate
means that the policy network has a still target to aim at for a while before the target changes, instead of the target changing ever step in the environment.
This is repeated for a specified number of steps. Over time, the policy should become stronger.
9 dqn.py
现在培训已经解决,这是整个dqn.py文件的代码。
import numpy as np
import tensorflow as tf
import random
from matplotlib import pyplot as plt
def build_dense_policy_nn():
def f(action_n):
model = tf.keras.models.Sequential([
tf.keras.layers.Dense(256, activation="relu"),
tf.keras.layers.Dense(128, activation="relu"),
tf.keras.layers.Dense(64, activation="relu"),
tf.keras.layers.Dense(32, activation="relu"),
tf.keras.layers.Dense(action_n, activation="linear"),
])
model.compile(loss=tf.keras.losses.MeanSquaredError(), optimizer=tf.keras.optimizers.Adam(0.0001))
return model
return f
class DQN:
def __init__(self, action_n, model):
self.action_n = action_n
self.policy = model(action_n)
self.target = model(action_n)
self.replay = []
self.max_replay_size = 10000
self.weights_initialised = False
def play_episode(self, env, epsilon, max_timesteps):
obs = env.reset()
rewards = 0
steps = 0
for _ in range(max_timesteps):
rand = np.random.uniform(0, 1)
if rand <= epsilon:
action = env.action_space.sample()
else:
actions = self.policy(np.array([obs]).astype(float)).numpy()
action = np.argmax(actions)
if not self.weights_initialised:
self.target.set_weights(self.policy.get_weights())
self.weights_initialised = True
new_obs, reward, done, _ = env.step(action)
if len(self.replay) >= self.max_replay_size:
self.replay = self.replay[(len(self.replay) - self.max_replay_size) + 1:]
self.replay.append([obs, action, reward, new_obs, done])
rewards += reward
obs = new_obs
steps += 1
yield steps, rewards
if done:
env.close()
break
def learn(self, env, timesteps, train_every = 5, update_target_every = 50, show_every_episode = 4, batch_size = 64, discount = 0.8, min_epsilon = 0.05, min_reward=150):
max_episode_timesteps = 1000
episodes = 1
epsilon = 1
decay = np.e ** (np.log(min_epsilon) / (timesteps * 0.85))
steps = 0
episode_list = []
rewards_list = []
while steps < timesteps:
for ep_len, rewards in self.play_episode(env, epsilon, max_episode_timesteps):
epsilon *= decay
steps += 1
if steps % train_every == 0 and len(self.replay) > batch_size:
batch = random.sample(self.replay, batch_size)
obs = np.array([o[0] for o in batch])
new_obs = np.array([o[3] for o in batch])
curr_qs = self.policy(obs).numpy()
future_qs = self.target(new_obs).numpy()
for row in range(len(batch)):
action = batch[row][1]
reward = batch[row][2]
done = batch[row][4]
if not done:
curr_qs[row][action] = reward + discount * np.max(future_qs[row])
else:
curr_qs[row][action] = reward
self.policy.fit(obs, curr_qs, batch_size=batch_size, verbose=0)
if steps % update_target_every == 0 and len(self.replay) > batch_size:
self.target.set_weights(self.policy.get_weights())
episodes += 1
if episodes % show_every_episode == 0:
print ("epsiode: ", episodes)
print ("explore rate: ", epsilon)
print ("episode reward: ", rewards)
print ("episode length: ", ep_len)
print ("timesteps done: ", steps)
if rewards > min_reward:
self.policy.save(f"policy-model-{rewards}")
episode_list.append(episodes)
rewards_list.append(rewards)
self.policy.save("policy-model-final")
plt.plot(episode_list, rewards_list)
plt.show()
def play(self, env):
for _ in range(10):
obs = env.reset()
done = False
while not done:
actions = self.policy(np.array([obs]).astype(float)).numpy()
action = np.argmax(actions)
obs, _, done, _ = env.step(action)
env.render()
def load(self, path):
m = tf.keras.models.load_model(path)
self.policy = m
play 是显示Agent In Action!
的方法load 将保存的DQN加载到类中
测试!
import gym
from dqn import *
env = gym.make("LunarLander-v2")
dqn = DQN(4, build_dense_policy_nn())
dqn.play(env)
dqn.learn(env, 70000)
dqn.play(env)
在训练之前,代理商会这样扮演...
在培训期间,我们可以看到进展如何...
epsiode: 4
explore rate: 0.9868456446936881
episode reward: -124.58158870915031
episode length: 71
timesteps done: 263
epsiode: 8
explore rate: 0.9661965615592099
episode reward: -120.64909734406406
episode length: 101
timesteps done: 683
epsiode: 12
explore rate: 0.9492716348733212
episode reward: -115.3412820349026
episode length: 103
timesteps done: 1034
epsiode: 16
explore rate: 0.9321267977756045
episode reward: -93.92673345696777
episode length: 85
timesteps done: 1396
...
epsiode: 44
explore rate: 0.8147960354481776
episode reward: -81.70688741109889
episode length: 87
timesteps done: 4068
epsiode: 48
explore rate: 0.8007650685225999
episode reward: -134.96785569534904
episode length: 95
timesteps done: 4413
epsiode: 52
explore rate: 0.7822352926206606
episode reward: -252.0391992426531
episode length: 117
timesteps done: 4878
epsiode: 56
explore rate: 0.7682233340884487
episode reward: -129.31041070395162
episode length: 118
timesteps done: 5237
epsiode: 60
explore rate: 0.7510891766906618
episode reward: -42.51701614323742
episode length: 150
timesteps done: 5685
...
epsiode: 200
explore rate: 0.05587076853211827
episode reward: -100.11491946673415
episode length: 1000
timesteps done: 57295
epsiode: 204
explore rate: 0.045679405591051145
episode reward: -107.24645551050241
episode length: 1000
timesteps done: 61295
epsiode: 208
explore rate: 0.040104832222074366
episode reward: -16.873940050515692
episode length: 1000
timesteps done: 63880
epsiode: 212
explore rate: 0.03278932696585445
episode reward: 116.37994616097882
episode length: 1000
timesteps done: 67880
epsiode: 216
explore rate: 0.03008289932359156
episode reward: -200.89010177116512
episode length: 354
timesteps done: 69591
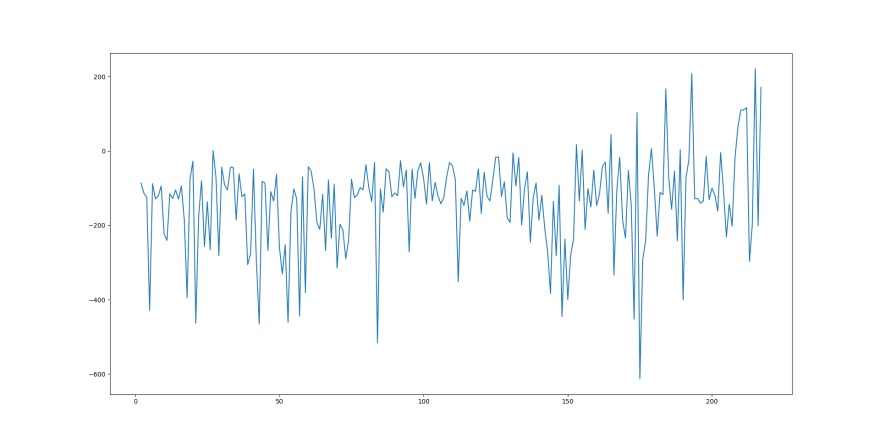
和此Evistion-VS-Reward Graph ...
您可能希望会有更明显的趋势,显示随着时间的推移的奖励增加。但是,由于勘探率,这种趋势被扭曲。随着发作的继续,勘探率下降,因此随着时间的推移,预期的奖励趋势变得更加明显。
这是代理在训练过程结束时的执行方式!
它仍然可以通过更平滑的着陆来处理,但我认为这是一个很好的表现。
也许您可以自己尝试一下,并调整一些培训参数,看看它们产生了什么结果!